题目

你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

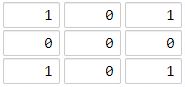
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

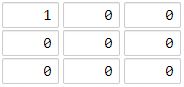
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] 不是 0 就是 1

思路

Queue<int[]> queue = new ArrayDeque<>();

解法

class Solution {
    public int maxDistance(int[][] grid) {
        int[] dx = {0, 0, 1, -1};
        int[] dy = {1, -1, 0, 0};

        Queue<int[]> queue = new ArrayDeque<>();
        int m = grid.length, n = grid[0].length;
        // 先把所有的陆地都入队。
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    queue.offer(new int[] {i, j});
                }
            }
        }

        // 从各个陆地开始，一圈一圈的遍历海洋，最后遍历到的海洋就是离陆地最远的海洋。
        boolean hasOcean = false;
        int[] point = null;
        while (!queue.isEmpty()) {
            point = queue.poll();
            int x = point[0], y = point[1];
            // 取出队列的元素，将其四周的海洋入队。
            for (int i = 0; i < 4; i++) {
                int newX = x + dx[i];
                int newY = y + dy[i];
                if (newX < 0 || newX >= m || newY < 0 || newY >= n || grid[newX][newY] != 0) {
                    continue;
                }
                grid[newX][newY] = grid[x][y] + 1; // 这里我直接修改了原数组，因此就不需要额外的数组来标志是否访问
                hasOcean = true;
                queue.offer(new int[] {newX, newY});
            }
        }

        // 没有陆地或者没有海洋，返回-1。
        if (point == null || !hasOcean) {
            return -1;
        }

        // 返回最后一次遍历到的海洋的距离。
        return grid[point[0]][point[1]] - 1;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现