题目

不使用任何库函数，设计一个 跳表 。

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

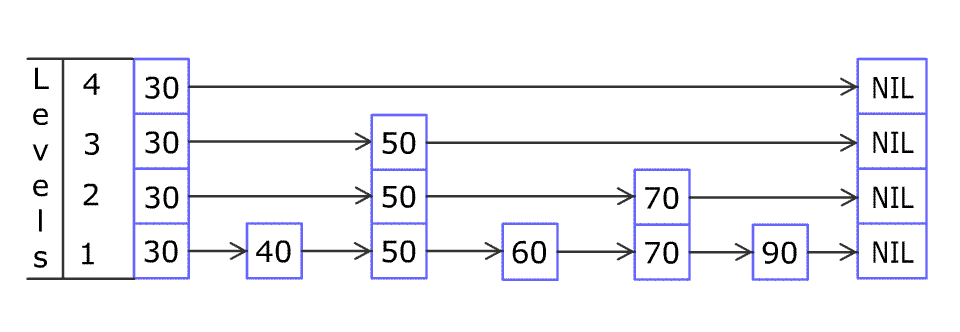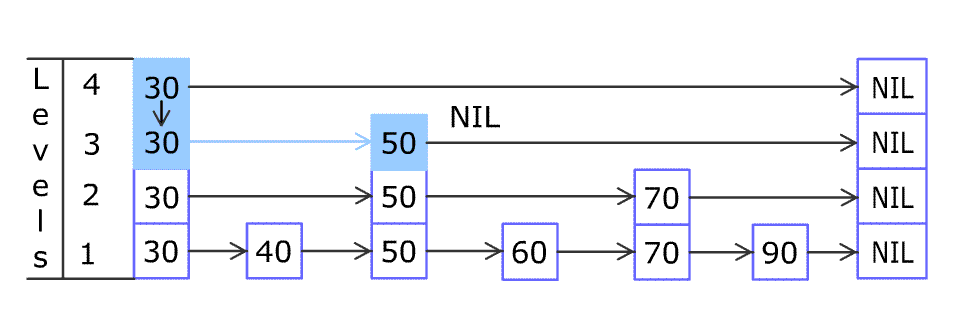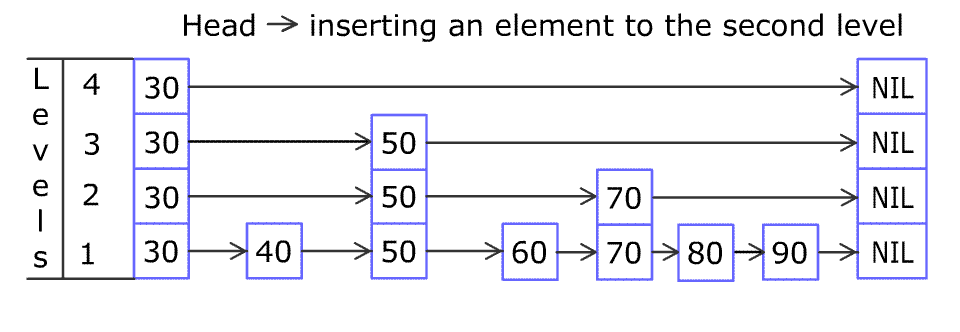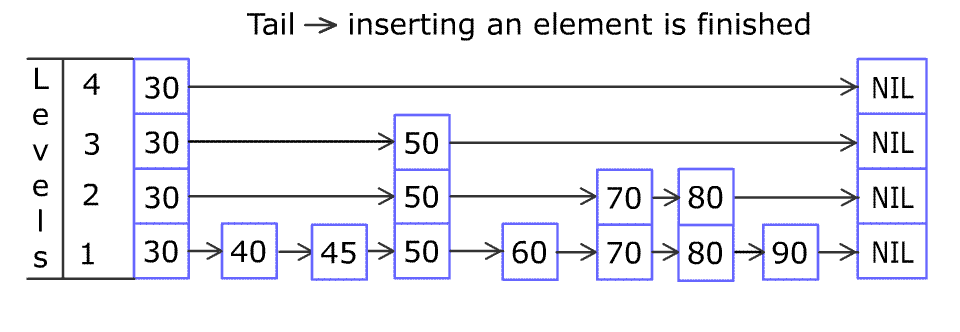
例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://en.wikipedia.org/wiki/Skip_list

在本题中，你的设计应该要包含这些函数：

• bool search(int target) : 返回target是否存在于跳表中。
• void add(int num): 插入一个元素到跳表。
• bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。
• 注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

- 输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

- 解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

提示:

• 0 <= num, target <= 2 * 10⁴
• 调用search, add, erase操作次数不大于 5 * 10⁴

思路

关键在于理解这种数据结构的思想
及随机层次的使用，避免变成线性链表
理解起来还是要花一些时间的，理解了写起来就容易多了

解法

class Skiplist {
        final int maxLevel = 5;

        Random random = new Random();

        SkipNode head = new SkipNode(-1, maxLevel); //头节点

        int level = 1; // 当前的层级，默认有一层

        class SkipNode {
            int val;
            SkipNode[] forwards;

            public SkipNode(int val, int level) {
                this.val = val;
                forwards = new SkipNode[level];
            }
        }

        public boolean search(int target) {
            SkipNode current = head;
            for (int i = level -1; i >= 0; i--) {
                while (current.forwards[i] != null && (current.forwards[i].val < target)) {
                    current = current.forwards[i];
                }
            }
            return current.forwards[0] != null && current.forwards[0].val == target;
        }

        public boolean erase(int num) {
            // 记录跳表中每一个层级的前序位置
            SkipNode[] levelPres = new SkipNode[maxLevel];
            SkipNode current = head;
            for (int i = level -1; i >= 0; i--) {
                while (current.forwards[i] != null && (current.forwards[i].val < num)) {
                    current = current.forwards[i];
                }
                levelPres[i] = current;
            }
            SkipNode removeData = levelPres[0].forwards[0];
            if (removeData == null || removeData.val != num) {
                return false;
            }
            for (int i = 0; i < level; i++) {
                if (levelPres[i].forwards[i] != removeData) {
                    break;
                }
                levelPres[i].forwards[i] = removeData.forwards[i];
            }
            // 更新当前的 level
            while (level > 1 && head.forwards[level - 1] == null) {
                level--;
            }
            return true;
        }

        public void add(int num) {
            // 记录跳表中每一个层级的前序位置
            SkipNode[] levelPres = new SkipNode[maxLevel];
            Arrays.fill(levelPres, head);

            SkipNode current = head;
            // 当前使用的层级 i 遍历每一层
            for (int i = level -1 ; i >= 0 ; i--) {
                // 遍历当前层级小于传入数据中最大的一个元素，即当前层级可以插入的位置的后面
                while (current.forwards[i] !=null && current.forwards[i].val < num) {
                    current = current.forwards[i];
                }
                levelPres[i] = current;
            }

            // 当前数据需要落到第几层
            int lv = randomLv();
            // 当前最大的层级数需要更新一下
            level = Math.max(lv, level);

            SkipNode newNode = new SkipNode(num, lv);
            for (int i = 0; i < lv; i++) {
                newNode.forwards[i] = levelPres[i].forwards[i];
                levelPres[i].forwards[i] = newNode;
            }
        }

        private int randomLv() {
          return random.nextInt(maxLevel) + 1;
        }

}

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist obj = new Skiplist();
 * boolean param_1 = obj.search(target);
 * obj.add(num);
 * boolean param_3 = obj.erase(num);
 */

总结

• 分析出几种情况，然后分别对各个情况实现