题目

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

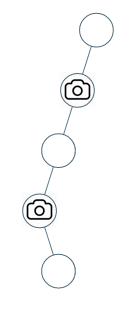
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

注意

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

思路

0：表示当前节点无覆盖 1：表示当前节点有摄像头 2：表示当前节点有覆盖

解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int count = 0;
    public int minCameraCover(TreeNode root) {
        if(dfs(root)==0){//若头结点的左右子节点都属于有覆盖的情况，那么头结点需要放置一个摄像头
            count++;
        }
        return count;
    }
    public int dfs(TreeNode node){

//遇到空节点当做有覆盖的情况。理想情况是叶子结点的父节点放摄像头可以使摄像头数量最少。
//如果将空节点当做有摄像头，那么摄像头的数量会非常多；如果将空节点当做无覆盖，那么叶子结点就都需要放摄像头,摄像头数量也会很多。
        if(node==null){
            return 2;
        }
        //后序遍历
        int left = dfs(node.left);
        int right = dfs(node.right);

//当左右子节点均为有覆盖的情况，当前节点返回无覆盖，这样就能让当前节点的父节点放摄像头，而不是在当前节点放摄像头，进而节省摄像头数量
        if(left==2&&right==2){
            return 0;
        }

//当左右子节点至少一个为无覆盖情况，那么当前节点必须放摄像头
        if(left==0||right==0){
            count++;
            return 1;
        }

//通过前面两个if的判断，说明当前节点的左右子节点都不是无覆盖情况，也不都是有覆盖情况，说明左右子节点的情况为 两个1 或者 一个1、一个2，此时当前节点返回有覆盖
        if(left==1||right==1){
            return 2;
        }

// 这个 return -1 逻辑不会走到这里。
        return -1;
    }}