题目

给你一棵有 n 个节点的无向树，节点编号为 0 到 n-1 ，它们中有一些节点有苹果。通过树上的一条边，需要花费 1 秒钟。

你从 节点 0 出发，请你返回最少需要多少秒，可以收集到所有苹果，并回到节点 0 。

无向树的边由 edges 给出，其中 edges[i] = [fromi, toi] ，表示有一条边连接 from 和 toi 。

除此以外，还有一个布尔数组 hasApple ，其中 hasApple[i] = true 代表节点 i 有一个苹果，否则，节点 i 没有苹果。

示例 1：

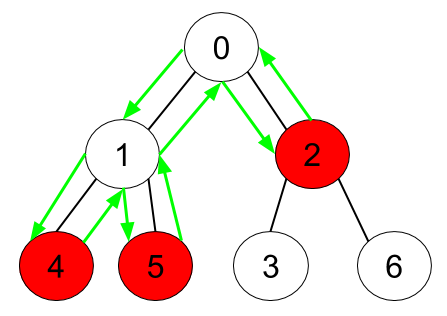
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple =
[false,false,true,false,true,true,false] 输出：8
解释：上图展示了给定的树，其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。

示例 2：

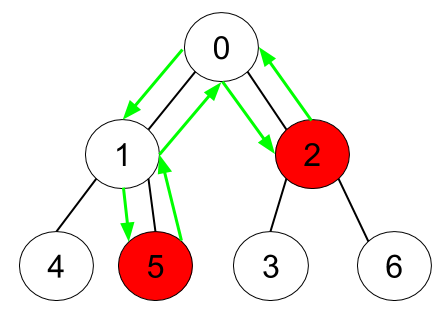
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
输出：6
解释：上图展示了给定的树，其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。

示例 3：

输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
输出：0

提示：

• 1 <= n <= 10^5
• edges.length == n-1
• edges[i].length == 2
• 0 <= fromi, toi <= n-1
• fromi < toi
• hasApple.length == n

思路

dfs从上往下遍历每个节点，自己或者孩子有苹果返回值就加一，因为肯定要经过这个节点

解法

class Solution {
    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {

        HashMap<Integer,List<Integer>> map = new HashMap<>();

        for(int[] edge : edges){
            List<Integer> list = map.getOrDefault(edge[0],new ArrayList<Integer>());
            list.add(edge[1]);
            map.put(edge[0],list);

            List<Integer> list1 = map.getOrDefault(edge[1],new ArrayList<Integer>());
            list1.add(edge[0]);
            map.put(edge[1],list1);
        }

        int ret = dfs(0,map,hasApple,new boolean[n+1]);
        return ret<1?ret:(ret-1)*2;

    }
    public int dfs(int node, HashMap<Integer, List<Integer>> map, List<Boolean> hasApple, boolean[] visited){
        visited[node] = true;
        List<Integer> child = map.getOrDefault(node, new ArrayList<Integer>());
        int res = 0;
        for(Integer next : child){
            if(!visited[next]) res += dfs(next, map, hasApple, visited);
        }
        if(hasApple.get(node) || res != 0) return res + 1;
        return 0;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现