 最小高度树Java
最小高度树Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
示例 1:
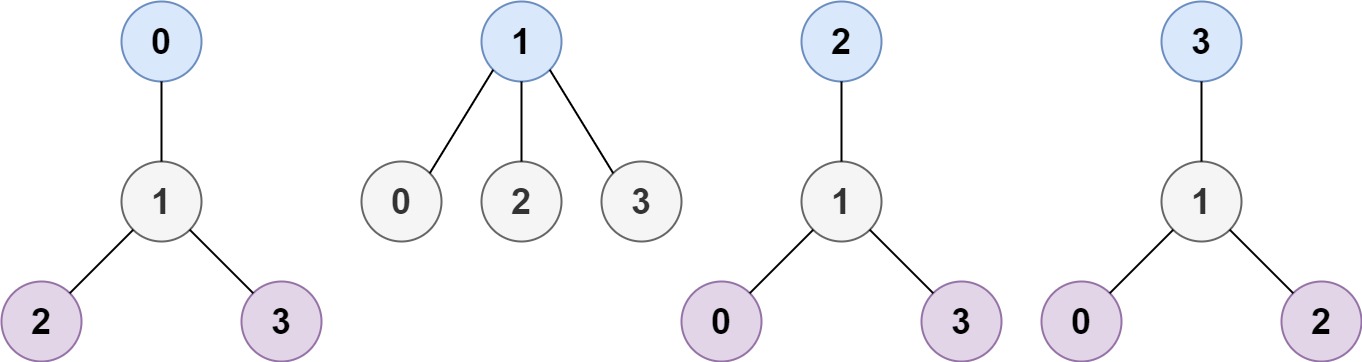
输入:n = 4, edges = [[1,0],[1,2],[1,3]]
输出:[1]
解释:如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。
示例 2:
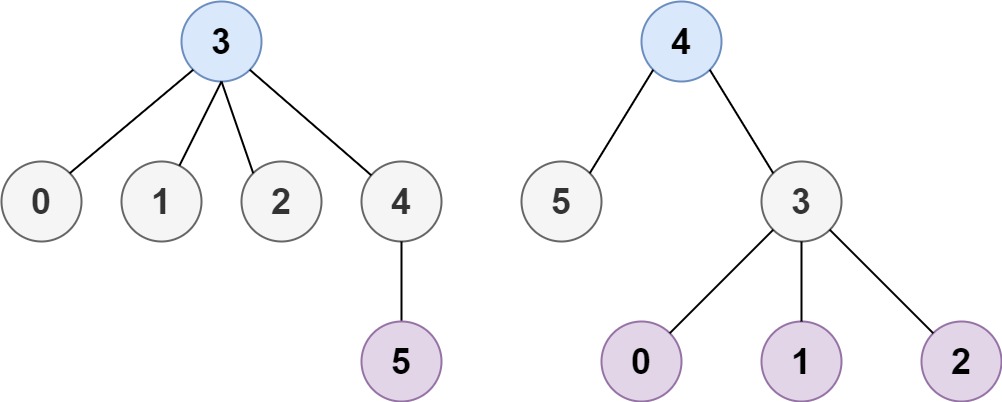
输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出:[3,4]
提示:
- 1 <= n <= 2 * 104
- edges.length == n - 1
- 0 <= ai, bi < n
- ai != bi
- 所有 (ai, bi) 互不相同
- 给定的输入 保证 是一棵树,并且 不会有重复的边
# 思路
构建图,逐步去除度为 1 的结点,最后一轮就是需要返回的答案。
# 解法
class Solution {
// 构建图,逐步去除度为 1 的结点,最后一轮就是需要返回的答案。
Map<Integer,List<Integer>> map = new HashMap<>();
List<Integer> ans = new ArrayList<>();
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1) {
ans.add(0);
return ans;
}
int[] count = new int[n];
for (int[] position : edges) {
int from = position[0];
int to = position[1];
map.putIfAbsent(from,new ArrayList<>());
map.putIfAbsent(to,new ArrayList<>());
map.get(from).add(to);
map.get(to).add(from);
count[from]++;
count[to]++;
}
Queue<Integer> queue = new LinkedList<>();
boolean[] visited = new boolean[n];
for (int i = 0; i < n; i++) {
if (count[i] == 1) {
queue.offer(i);
visited[i] = true;
}
}
while (!queue.isEmpty()) {
int len = queue.size();
if (len == n) break;
while (len-- > 0) {
int index = queue.poll();
n--;
count[index]--;
for (int next : map.get(index)) {
if (visited[next] == true) continue;
count[next]--;
if (count[next] == 1) {
queue.offer(next);
visited[next] = true;
}
}
}
}
while (!queue.isEmpty()) ans.add(queue.poll());
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# 总结
- 分析出几种情况,然后分别对各个情况实现


