题目

在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

输入：edges = [[1,2],[1,3],[2,3]] 输出：[2,3] 示例 2：

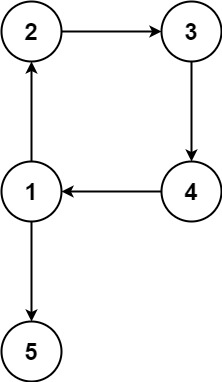
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]] 输出：[4,1]

提示：

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ui, vi <= n

思路

    // 寻找是否存在入度为 2 的顶点

    // 如果存在入度为 2 的顶点
    // 尝试删除指向该顶点的某一条边，看剩下的点是否能够构成树
    // 如果可以构成树，直接返回该边，否则返回另一条边

    Arrays.equals(e, remove)

解法

class Solution {
    
    int[] parent;
    public int[] findRedundantDirectedConnection(int[][] edges) {
        parent = new int[1001];
        int[] in = new int[1001];
        int[] res = {};
        // 寻找是否存在入度为 2 的顶点
        for (int[] e : edges) {
            if (++in[e[1]] == 2) {
                res = e;
            }
        }
        // 如果存在入度为 2 的顶点
        // 尝试删除指向该顶点的某一条边，看剩下的点是否能够构成树
        // 如果可以构成树，直接返回该边，否则返回另一条边
        if (res.length != 0) {
            if (check(edges, res)) return res;
            else {
                for (int[] e : edges) if (e[1] == res[1]) return e;
            }
        }
        // 重新初始化并查集
        for (int i = 0; i < 1001; i++) {
            parent[i] = i;
        }
        for (int[] e : edges) {
            // 删除加入形成环的边
            if (find(e[0]) == find(e[1])) return e;
            else union(e[0], e[1]);
        }
        return new int[0];
    }
    
    // 判断有向边构成的图形是否为树
    boolean check(int[][] edges, int[] remove) {
        // 初始化并查集
        for (int i = 0; i < 1001; i++) {
            parent[i] = i;
        }
        for (int[] e : edges) {
            // 跳过要删除的边
            if (Arrays.equals(e, remove)) continue;
            // 删除之后构成的图案不为树
            if (find(e[0]) == find(e[1])) return false;
            else union(e[0], e[1]);
        }
        return true;
    }

    int find(int x) {
        if (parent[x] != x) parent[x] = find(parent[x]);
        return parent[x];
    }

    void union(int x, int y) {
        if (find(x) != find(y)) parent[find(y)] = parent[x];
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现