1728. 猫和老鼠IIJava

文章发布较早，内容可能过时，阅读注意甄别。

# 题目

一只猫和一只老鼠在玩一个叫做猫和老鼠的游戏。

它们所处的环境设定是一个 rows x cols 的方格 grid ，其中每个格子可能是一堵墙、一块地板、一位玩家（猫或者老鼠）或者食物。

玩家由字符 'C' （代表猫）和 'M' （代表老鼠）表示。
地板由字符 '.' 表示，玩家可以通过这个格子。
墙用字符 '#' 表示，玩家不能通过这个格子。
食物用字符 'F' 表示，玩家可以通过这个格子。
字符 'C' ， 'M' 和 'F' 在 grid 中都只会出现一次。猫和老鼠按照如下规则移动：
老鼠先移动，然后两名玩家轮流移动。
每一次操作时，猫和老鼠可以跳到上下左右四个方向之一的格子，他们不能跳过墙也不能跳出 grid 。
catJump 和 mouseJump 是猫和老鼠分别跳一次能到达的最远距离，它们也可以跳小于最大距离的长度。
它们可以停留在原地。
老鼠可以跳跃过猫的位置。游戏有 4 种方式会结束：
如果猫跟老鼠处在相同的位置，那么猫获胜。
如果猫先到达食物，那么猫获胜。
如果老鼠先到达食物，那么老鼠获胜。
如果老鼠不能在 1000 次操作以内到达食物，那么猫获胜。给你 rows x cols 的矩阵 grid 和两个整数 catJump 和 mouseJump ，双方都采取最优策略，如果老鼠获胜，那么请你返回 true ，否则返回 false 。

示例 1：

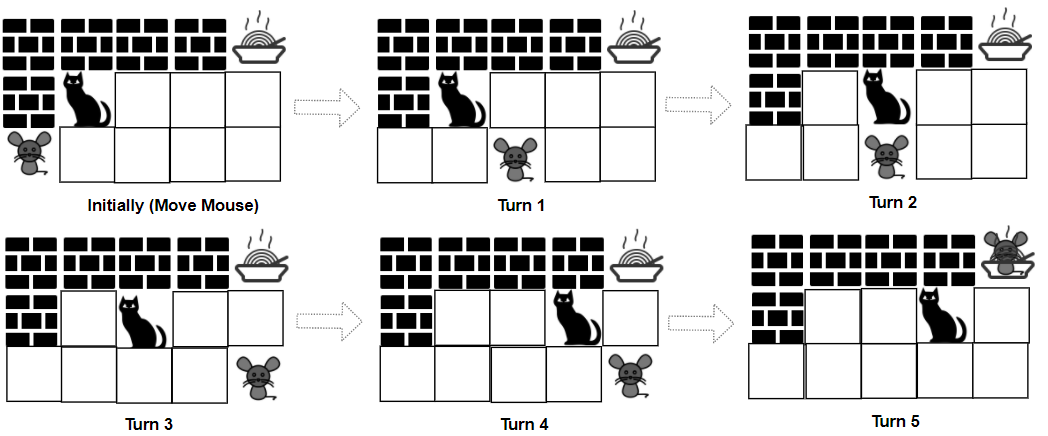
输入：grid = ["####F","#C...","M...."], catJump = 1, mouseJump = 2
输出：true
解释：猫无法抓到老鼠，也没法比老鼠先到达食物。

示例 2：

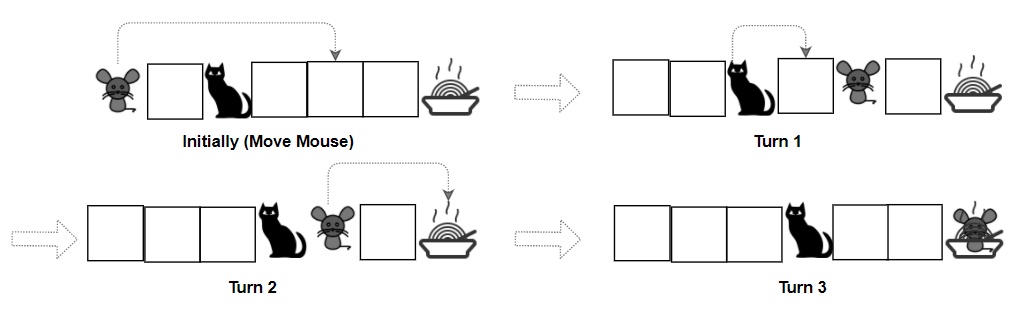
输入：grid = ["M.C...F"], catJump = 1, mouseJump = 4
输出：true

示例 3：

输入：grid = ["M.C...F"], catJump = 1, mouseJump = 3
输出：false

示例 4：

输入：grid = ["C...#","...#F","....#","M...."], catJump = 2, mouseJump = 5
输出：false

示例 5：

输入：grid = [".M...","..#..","#..#.","C#.#.","...#F"], catJump = 3, mouseJump = 1
输出：true

提示：

rows == grid.length
cols = grid[i].length
1 <= rows, cols <= 8
grid[i][j] 只包含字符 'C' ，'M' ，'F' ，'.' 和 '#' 。
grid 中只包含一个 'C' ，'M' 和 'F' 。
1 <= catJump, mouseJump <= 8

# 思路

其实和1差不多的思路，就是更加复杂，还有注意0格也要计算其中

# 解法

class Solution {
    public boolean canMouseWin(String[] grid, int catJump, int mouseJump) {
        int r = grid.length, c = grid[0].length();
        int FOOD = 0, CAT = 0, MOUSE = 0, CAT_TURE = 1, MOUSE_TURE = 0;
        int UNKNOWN = 0, CAT_WIN = 2, MOUSE_WIN = 1;
        int[][][] degrees = new int[r*c][r*c][2];
        int[][][] dp = new int[r*c][r*c][2];
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                char ch = grid[i].charAt(j);
                if (ch == 'F') FOOD = i*c + j;
                if (ch == 'C') CAT = i*c + j;
                if (ch == 'M') MOUSE = i*c + j;
            }
        }
        // 计算入度
        int[][][] ans = new int[r][c][2];
        int[] b = new int[c];
        int a = 0;
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                char ch = grid[i].charAt(j);
                if (ch == '#' || ch == 'F') {
                    a = 0;
                    b[j] = 0;
                } else {
                    ans[i][j][CAT_TURE] += Math.min(a, catJump);
                    ans[i][j][CAT_TURE] += Math.min(b[j], catJump);
                    ans[i][j][MOUSE_TURE] += Math.min(a, mouseJump);
                    ans[i][j][MOUSE_TURE] += Math.min(b[j], mouseJump);
                    a++;
                    b[j]++;
                }
            }
            a = 0;
        }
        a = 0;
        Arrays.fill(b, 0);
        for (int i = r-1; i >= 0; i--) {
            for (int j = c-1; j >= 0; j--) {
                char ch = grid[i].charAt(j);
                if (ch == '#' || ch == 'F') {
                    a = 0;
                    b[j] = 0;
                } else {
                    ans[i][j][CAT_TURE] += Math.min(a, catJump);
                    ans[i][j][CAT_TURE] += Math.min(b[j], catJump);
                    ans[i][j][MOUSE_TURE] += Math.min(a, mouseJump);
                    ans[i][j][MOUSE_TURE] += Math.min(b[j], mouseJump);
                    a++;
                    b[j]++;
                }
            }
            a = 0;
        }
        for (int i = 0; i < r*c; i++) {
            if (i == FOOD || grid[i/c].charAt(i%c) == '#') continue;
            for (int j = 0; j < r*c; j++) {
                if (j == FOOD || grid[j/c].charAt(j%c) == '#' || i == j) continue;
                int catX = j/c, catY = j%c, mouseX = i/c, mouseY = i%c;
                // + 1 是因为移动0格得情况
                degrees[i][j][CAT_TURE] = ans[catX][catY][CAT_TURE] + 1;
                degrees[i][j][MOUSE_TURE] = ans[mouseX][mouseY][MOUSE_TURE] + 1;
            }
        }
        Deque<int[]> q = new ArrayDeque<>();
        // 老鼠赢
        for (int i = 0; i < r*c; i++) {
            if (i == FOOD || grid[i/c].charAt(i%c) == '#') continue;
            dp[FOOD][i][CAT_TURE] = MOUSE_WIN;
            dp[FOOD][i][MOUSE_TURE] = MOUSE_WIN;
            q.add(new int[]{FOOD, i, CAT_TURE});
        }
        // 猫赢
        for (int i = 0; i < r*c; i++) {
            if (i == FOOD || grid[i/c].charAt(i%c) == '#') continue;
            dp[i][FOOD][CAT_TURE] = CAT_WIN;
            dp[i][FOOD][MOUSE_TURE] = CAT_WIN;
            dp[i][i][CAT_TURE] = CAT_WIN;
            dp[i][i][MOUSE_TURE] = CAT_WIN;
            q.add(new int[]{i, FOOD, MOUSE_TURE});
            q.add(new int[]{i, i, MOUSE_TURE});
        }
        while (!q.isEmpty()) {
            int[] poll = q.poll();
            int x = poll[2] == CAT_TURE ? poll[0]/c : poll[1]/c, y = poll[2] == CAT_TURE ? poll[0]%c : poll[1]%c;
            int jump = poll[2] == CAT_TURE ? mouseJump : catJump;
            // 不动
            if (dp[poll[0]][poll[1]][poll[2] == CAT_TURE ? MOUSE_TURE : CAT_TURE] == UNKNOWN) {
                int[] next = new int[]{poll[0], poll[1], poll[2] == CAT_TURE ? MOUSE_TURE : CAT_TURE};
                // 必赢
                if ((dp[poll[0]][poll[1]][poll[2]] == CAT_WIN && poll[2] == MOUSE_TURE) ||
                        dp[poll[0]][poll[1]][poll[2]] == MOUSE_WIN && poll[2] == CAT_TURE) {
                    dp[next[0]][next[1]][next[2]] = dp[poll[0]][poll[1]][poll[2]];
                    q.add(next);
                } // 必输得一种情况
                else {
                    // 所有都是必输，则当前必输
                    if (--degrees[next[0]][next[1]][next[2]] == 0) {
                        dp[next[0]][next[1]][next[2]] = next[2] == CAT_TURE ? MOUSE_WIN : CAT_WIN;
                        q.add(next);
                    }
                }
            }
            // 向上
            for (int i = 1; i <= jump && x-i >= 0; i++) {
                if (grid[x-i].charAt(y) == '#' || grid[x-i].charAt(y) == 'F') break;
                int[] next = poll[2] == CAT_TURE ? new int[]{(x-i)*c + y, poll[1], MOUSE_TURE} : new int[]{poll[0], (x-i)*c + y, CAT_TURE};
                if (dp[next[0]][next[1]][next[2]] != UNKNOWN) continue;
                // 必赢
                if ((dp[poll[0]][poll[1]][poll[2]] == CAT_WIN && poll[2] == MOUSE_TURE) ||
                        dp[poll[0]][poll[1]][poll[2]] == MOUSE_WIN && poll[2] == CAT_TURE) {
                    dp[next[0]][next[1]][next[2]] = dp[poll[0]][poll[1]][poll[2]];
                    q.add(next);
                } // 必输得一种情况
                else {
                    // 所有都是必输，则当前必输
                    if (--degrees[next[0]][next[1]][next[2]] == 0) {
                        dp[next[0]][next[1]][next[2]] = next[2] == CAT_TURE ? MOUSE_WIN : CAT_WIN;
                        q.add(next);
                    }
                }
            }
            // 向右
            for (int i = 1; i <= jump && y+i < c; i++) {
                if (grid[x].charAt(y+i) == '#' || grid[x].charAt(y+i) == 'F') break;
                int[] next = poll[2] == CAT_TURE ? new int[]{x*c + y+i, poll[1], MOUSE_TURE} : new int[]{poll[0], x*c + y+i, CAT_TURE};
                if (dp[next[0]][next[1]][next[2]] != UNKNOWN) continue;
                // 必赢
                if ((dp[poll[0]][poll[1]][poll[2]] == CAT_WIN && poll[2] == MOUSE_TURE) ||
                        dp[poll[0]][poll[1]][poll[2]] == MOUSE_WIN && poll[2] == CAT_TURE) {
                    dp[next[0]][next[1]][next[2]] = dp[poll[0]][poll[1]][poll[2]];
                    q.add(next);
                } // 必输得一种情况
                else {
                    // 所有都是必输，则当前必输
                    if (--degrees[next[0]][next[1]][next[2]] == 0) {
                        dp[next[0]][next[1]][next[2]] = next[2] == CAT_TURE ? MOUSE_WIN : CAT_WIN;
                        q.add(next);
                    }
                }
            }
            // 向下
            for (int i = 1; i <= jump && x+i < r; i++){
                if (grid[x+i].charAt(y) == '#' || grid[x+i].charAt(y) == 'F') break;
                int[] next = poll[2] == CAT_TURE ? new int[]{(x+i)*c + y, poll[1], MOUSE_TURE} : new int[]{poll[0], (x+i)*c + y, CAT_TURE};
                if (dp[next[0]][next[1]][next[2]] != UNKNOWN) continue;
                // 必赢
                if ((dp[poll[0]][poll[1]][poll[2]] == CAT_WIN && poll[2] == MOUSE_TURE) ||
                        dp[poll[0]][poll[1]][poll[2]] == MOUSE_WIN && poll[2] == CAT_TURE) {
                    dp[next[0]][next[1]][next[2]] = dp[poll[0]][poll[1]][poll[2]];
                    q.add(next);
                } // 必输得一种情况
                else {
                    // 所有都是必输，则当前必输
                    if (--degrees[next[0]][next[1]][next[2]] == 0) {
                        dp[next[0]][next[1]][next[2]] = next[2] == CAT_TURE ? MOUSE_WIN : CAT_WIN;
                        q.add(next);
                    }
                }
            }
            // 向左
            for (int i = 1; i <= jump && y-i >= 0; i++) {
                if (grid[x].charAt(y-i) == '#' || grid[x].charAt(y-i) == 'F') break;
                int[] next = poll[2] == CAT_TURE ? new int[]{x*c + y-i, poll[1], MOUSE_TURE} : new int[]{poll[0], x*c + y-i, CAT_TURE};
                if (dp[next[0]][next[1]][next[2]] != UNKNOWN) continue;
                // 必赢
                if ((dp[poll[0]][poll[1]][poll[2]] == CAT_WIN && poll[2] == MOUSE_TURE) ||
                        dp[poll[0]][poll[1]][poll[2]] == MOUSE_WIN && poll[2] == CAT_TURE) {
                    dp[next[0]][next[1]][next[2]] = dp[poll[0]][poll[1]][poll[2]];
                    q.add(next);
                } // 必输得一种情况
                else {
                    // 所有都是必输，则当前必输
                    if (--degrees[next[0]][next[1]][next[2]] == 0) {
                        dp[next[0]][next[1]][next[2]] = next[2] == CAT_TURE ? MOUSE_WIN : CAT_WIN;
                        q.add(next);
                    }
                }
            }
        }
        return dp[MOUSE][CAT][MOUSE_TURE] == MOUSE_WIN;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185

# 总结

分析出几种情况，然后分别对各个情况实现

#Java