题目

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中 任何 一个。

示例 1：

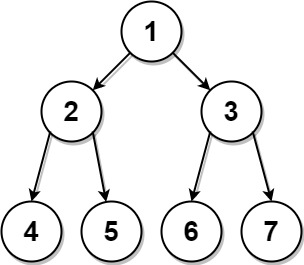
输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

示例 2:

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

注意

1 <= preorder.length <= 30
1 <= preorder[i] <= preorder.length
preorder 中所有值都 不同
postorder.length == preorder.length
1 <= postorder[i] <= postorder.length
postorder 中所有值都 不同
保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

思路

确定根节点，左节点长度，右节点长度等

解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /*
    改进:索引代替新数组
     */
    int[] preorder;
    int[] postorder;
    public TreeNode constructFromPrePost(int[] _preorder, int[] _postorder) {
        preorder = _preorder;
        postorder = _postorder;
        return dfs(0, preorder.length - 1, 0, postorder.length - 1);
    }
    /*
    pre_start:前序遍历起始索引
    pre_end:前序遍历结束索引
    post_start:后序遍历起始索引
    post_end:后序遍历结束索引
     */
    private TreeNode dfs(int pre_start, int pre_end, int post_start, int post_end) {
        // 区间无效返回null
        if (pre_start > pre_end) return null;
        int len = pre_end - pre_start + 1;
        TreeNode root = new TreeNode(preorder[pre_start]);
        // 当区间长度为1时,可以直接返回该节点作为根节点
        if (len == 1) {
            return root;
        }
        // 到这里都是节点个数>1的情况,但是根节点还是可以轻易得出
        // 再进行左右子节点的连接
        int index = post_start;
        // 让index停留在postorder[index] == preorder[1]处
        while (index <= post_end && postorder[index] != preorder[pre_start + 1]) {
            index++;
        }
        // 分割左右子树
        // 左子树长度
        int leftCount = index - post_start + 1;
        // 建立连接:这里建议画个图比较好理解->注意这里的pre部分要用pre部分算;post部分要用post部分算
        // 结合一下pre_start与post_start;pre_end与post_end
        root.left = dfs(pre_start + 1, pre_start + leftCount, post_start, post_start + leftCount - 1);  // 左子树前序遍历区间始末索引与后序遍历区间始末索引
        root.right = dfs(pre_start + leftCount + 1, pre_end, post_start + leftCount, post_end - 1); // 右子树前序遍历区间始末索引与后序遍历区间始末索引
        // 最后别忘了返回根节点
        return root;
    }
}