多米诺和托米诺平铺Java
文章发布较早，内容可能过时，阅读注意甄别。
# 题目
有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例 1:
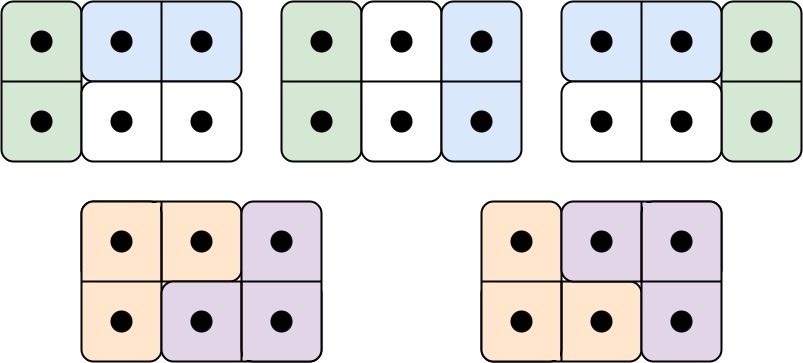
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:
输入: n = 1
输出: 1
提示：
- 1 <= n <= 1000
# 思路
// 递推式：f(n) = 2 * f(n-1) + f(n-3)
# 解法
class Solution {
// 递推式：f(n) = 2 * f(n-1) + f(n-3)
public int numTilings(int N) {
if(N == 1)
return 1;
if(N == 2)
return 2;
if(N == 3)
return 5;
int n_3 = 1;
int n_2 = 2;
int n_1 = 5;
int temp = 0;
for (int i = 4; i <= N; i++) {
temp = (2 * n_1) % 1000000007 + n_3 % 1000000007 ;
n_3 = n_2;
n_2 = n_1;
n_1 = temp % 1000000007 ;
}
return n_1;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 总结
- 分析出几种情况，然后分别对各个情况实现
