奇怪的打印机IIJava

文章发布较早，内容可能过时，阅读注意甄别。

# 题目

给你一个奇怪的打印机，它有如下两个特殊的打印规则：

每一次操作时，打印机会用同一种颜色打印一个矩形的形状，每次打印会覆盖矩形对应格子里原本的颜色。
一旦矩形根据上面的规则使用了一种颜色，那么相同的颜色不能再被使用。给你一个初始没有颜色的 m x n 的矩形 targetGrid ，其中 targetGrid[row][col] 是位置 (row, col) 的颜色。

如果你能按照上述规则打印出矩形 targetGrid ，请你返回 true ，否则返回 false 。

示例 1：

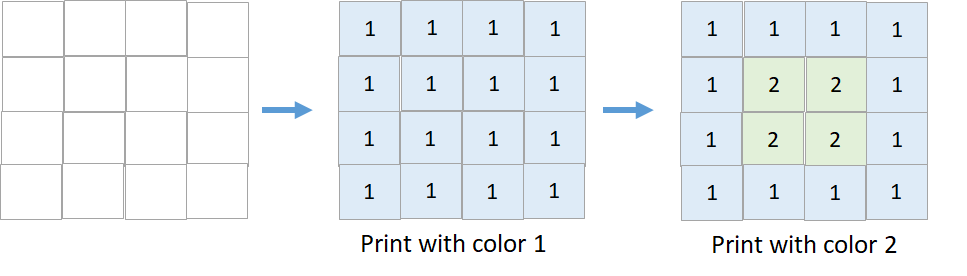
输入：targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
输出：true

示例 2：

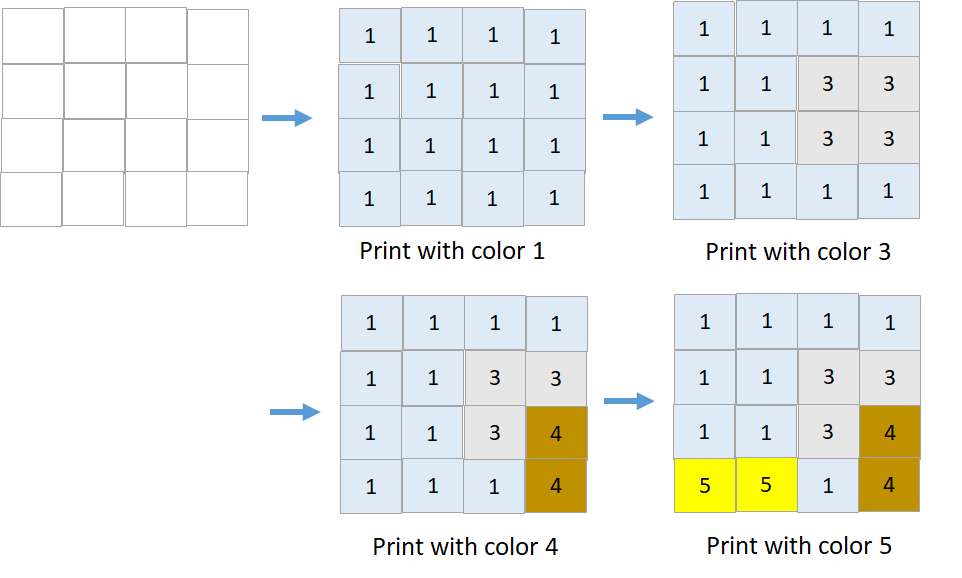
输入：targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
输出：true

示例 3：

输入：targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
输出：false
解释：没有办法得到 targetGrid ，因为每一轮操作使用的颜色互不相同。

示例 4：

输入：targetGrid = [[1,1,1],[3,1,3]]
输出：false

提示：

m == targetGrid.length
n == targetGrid[i].length
1 <= m, n <= 60
1 <= targetGrid[row][col] <= 60

# 思路

有向图采用邻接链表

# 解法


/*
1.将目标问题转换为有向图
在targetGrid中，首先求出每个像素的举行范围
在举行A中存在一个像素为B，则A应该先打印，B后打印，即A->B建立有向边，据此建立有向图

有向图采用邻接链表
顶点表示颜色
A->B表示颜色A先打印，颜色B后打印。颜色B在颜色A图层的上面

2.对有向图进行拓扑排序，有解，则说明可以从初始状态按照一系列打印规则打印到终止状态
*/
class Solution {
    public boolean isPrintable(int[][] targetGrid) {
        List[] adjList;
        int[] top=new int[61];
        int[] bottom=new int[61];
        int[] left=new int[61];
        int[] right=new int[61];
        int color;

        for(int i=1; i<=60; i++){
            top[i] = 61;
            bottom[i] = 0;
            left[i] = 61;
            right[i] = 0;
        }

        // 遍历图中的像素，求出每种颜色的矩形范围
        for(int r=0; r<targetGrid.length; r++){
            for(int c=0; c<targetGrid[0].length; c++){
                color = targetGrid[r][c];
                top[color] = Math.min(top[color], r);
                bottom[color] = Math.max(bottom[color], r);
                left[color] = Math.min(left[color], c);
                right[color] = Math.max(right[color], c);
            }
        }

        //建有向图
        adjList=new List[61]; // 用邻接链表的方式表示有向图
        boolean[][] haveEdge = new boolean[61][61]; // 判断是否已经有边，避免重复添加
        int[] indegree = new int[61];
        for(int i=1; i<=60; i++){
            adjList[i] = new ArrayList<Integer>();
        }
        for(int r=0; r<targetGrid.length; r++){
            for(int c=0; c<targetGrid[0].length; c++){
                color = targetGrid[r][c];
                for(int cl=1; cl<=60; cl++){
                    if(r>=top[cl] && r<=bottom[cl] && c>=left[cl] && c<=right[cl] && color!=cl &&haveEdge[color][cl]==false){
                        haveEdge[color][cl] = true;
                        indegree[cl]++;
                        adjList[color].add(cl);
                    }
                }
            }
        }

        // 进行拓扑排序，如果最后存在入度不为0的颜色，则不能打印
        int count = 0;
        Queue<Integer> queue = new LinkedList<>();
        for(int i=1; i<=60; i++){
            if(indegree[i]==0){
                queue.offer(i);
            }
        }
        while(!queue.isEmpty()){
            color = queue.poll();
            for(int i=0; i<adjList[color].size(); i++){
                int c = (Integer)adjList[color].get(i);
                indegree[c]--;
                if(indegree[c]==0){
                    queue.offer(c);
                }
            }
        }
        for(int i=1; i<=60; i++){
            if(indegree[i]>0){
                return false;
            }
        }
        return true;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

# 总结

分析出几种情况，然后分别对各个情况实现

#Java