题目

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

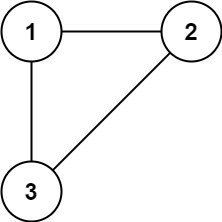
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

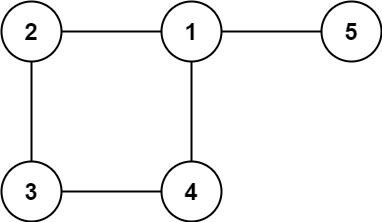
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• edges 中无重复元素
• 给定的图是连通的

思路

并查集 + 路径压缩

解法

class Solution {
    public int[] findRedundantConnection(int[][] edges) {

        int n = edges.length;
        int[] pre = new int[n + 1];
        //每个pre节点初始化为自己
        for(int i = 0;i<= n;i++){
            pre[i] = i;
        }
        for(int[] arr : edges){
            int root1 = findRoot(arr[0],pre);
            int root2 = findRoot(arr[1],pre);
            //arr边的两个节点arr[0],arr[1]有共同的根节点，说明在一个连通子图中，此时这条边不能加入，否则会形成环，因此这条边需要删去
            if(root1 == root2){
                return arr;
            }
            //并集，将root1下所有子节点的根节点设为root2，方便下次寻找根节点
            adjust(arr[0],root2,pre);
        }
        return new int[0];
    }
    //寻找该节点的根节点
    private int findRoot(int num,int[] pre){
        while(pre[num] != num){
            num = pre[num];
        }
        return num;
    }
    //并集 + 路径压缩
    private void adjust(int x,int root,int[] pre){
        while(pre[x] != root){
            int temp = pre[x];
            pre[x] = root;
            x = temp;
        }
    }
    
}

总结

• 分析出几种情况，然后分别对各个情况实现