所有可能的路径Java

文章发布较早，内容可能过时，阅读注意甄别。

# 题目

给你一个有 n 个节点的有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

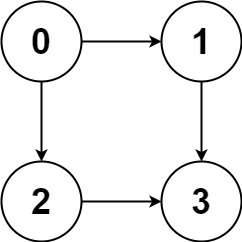
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

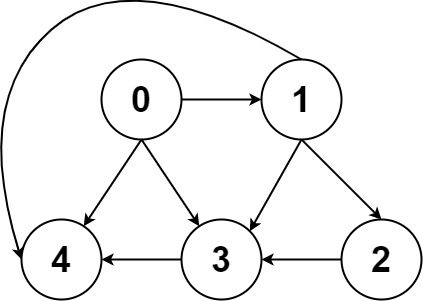
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素互不相同
保证输入为有向无环图（DAG）

# 思路

dfs

# 解法


class Solution {
    // 终止条件 直接res.add(list)不行，只能新new一个才行？
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> list = new ArrayList<>();
    int[][] g ;
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        g = graph;
        dfs(0,g[0]);
        return res;
    }
    public void dfs(int k,int[] a){
        list.add(k);
        if(k==g.length-1) {
            res.add(new ArrayList<>(list));//踩大坑，直接res.add(list)不行，只能新new一个才行？
            list.remove(list.size()-1);
            return;
        }
        for(int i = 0;i<a.length;i++){
                dfs(a[i],g[a[i]]);
        }
        list.remove(list.size()-1);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 总结

分析出几种情况，然后分别对各个情况实现