隔离病毒Java
文章发布较早，内容可能过时，阅读注意甄别。
# 题目
病毒扩散得很快，现在你的任务是尽可能地通过安装防火墙来隔离病毒。
假设世界由 m x n 的二维矩阵 isInfected 组成， isInfected[i][j] == 0 表示该区域未感染病毒，而 isInfected[i][j] == 1 表示该区域已感染病毒。可以在任意 2 个相邻单元之间的共享边界上安装一个防火墙（并且只有一个防火墙）。
每天晚上，病毒会从被感染区域向相邻未感染区域扩散，除非被防火墙隔离。现由于资源有限，每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域（一个区域或连续的一片区域），且该感染区域对未感染区域的威胁最大且 保证唯一 。
你需要努力使得最后有部分区域不被病毒感染，如果可以成功，那么返回需要使用的防火墙个数; 如果无法实现，则返回在世界被病毒全部感染时已安装的防火墙个数。
示例 1：
输入: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
输出: 10
解释:一共有两块被病毒感染的区域。
在第一天，添加 5 墙隔离病毒区域的左侧。病毒传播后的状态是:
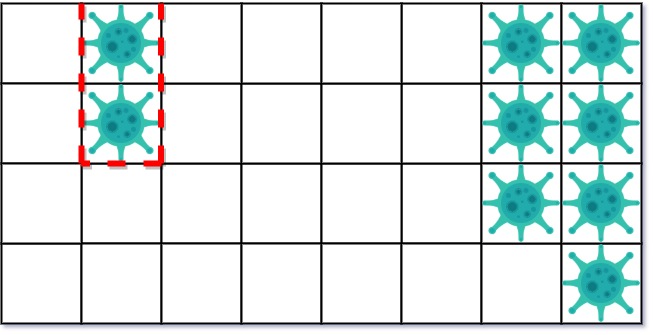第二天，在右侧添加 5 个墙来隔离病毒区域。此时病毒已经被完全控制住了。
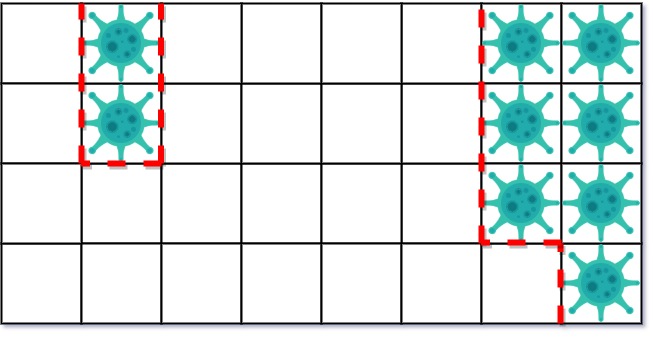示例 2：
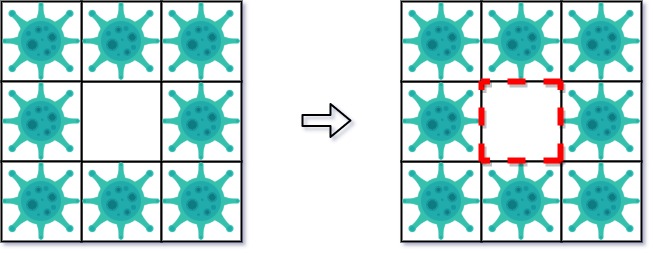
输入: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
输出: 4
解释: 虽然只保存了一个小区域，但却有四面墙。
注意，防火墙只建立在两个不同区域的共享边界上。
示例 3:
输入: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
输出: 13
解释: 在隔离右边感染区域后，隔离左边病毒区域只需要 2 个防火墙。
提示:
- m == isInfected.length
- n == isInfected[i].length
- 1 <= m, n <= 50
- isInfected[i][j] is either 0 or 1
- 在整个描述的过程中，总有一个相邻的病毒区域，它将在下一轮 严格地感染更多未受污染的方块
# 思路
# 解法
class Solution {
int[][] grid;
int m, n;
int willCount = 0; // 即将感染的格子
int wallCount = 0; // 每次需的隔离墙的数量
int[][] direct = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int res = 0;
public int containVirus(int[][] isInfected) {
grid = isInfected;
m = isInfected.length;
n = isInfected[0].length;
List<Region> regions = find();
while (regions.size() > 0) {
int idx = 0;
int maxWillCount = 0;
for (int i = 0; i < regions.size(); i++) {
int c = regions.get(i).willInfectedCount;
if (c > maxWillCount) {
idx = i;
maxWillCount = c;
}
}
for (int i = 0; i < regions.size(); i++) {
Region region = regions.get(i);
if (idx == i) updateBlockadedDfs(region.infected, region.i, region.j);
else updateInfectedDfs(region.infected, region.i, region.j);
System.out.println();
}
res += regions.get(idx).wallCount;
regions = find();
}
return res;
}
// 封锁
private void updateBlockadedDfs(int[][] temp, int i, int j) {
if (i < 0 || j < 0 || i >= m || j >= n) return;
// 已经遍历的 且 需要封锁
if (temp[i][j] == 2) {
grid[i][j] = -1;
temp[i][j] = -1;
for (int[] ints : direct) {
updateBlockadedDfs(temp, i + ints[0], j + ints[1]);
}
}
}
// 感染
private void updateInfectedDfs(int[][] temp, int i, int j) {
if (i < 0 || j < 0 || i >= m || j >= n) return;
boolean flag = temp[i][j] == 3;
// 已经遍历的 或 要感染的
if (temp[i][j] == 2 || temp[i][j] == 3) {
grid[i][j] = 1;
temp[i][j] = 1;
if (!flag)
for (int[] ints : direct) {
updateInfectedDfs(temp, i + ints[0], j + ints[1]);
}
}
}
private List<Region> find() {
List<Region> list = new ArrayList<>();
// 1. 统计所有病毒感染的区域
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int[][] temp = copyGrid(grid); // 2: 访问过的病毒区域 3: 未来要变成的病毒区域
dfs(temp, i, j);
// 构建region
Region region = new Region();
region.i = i;
region.j = j;
region.infected = temp;
region.wallCount = wallCount;
region.willInfectedCount = willCount;
list.add(region);
willCount = 0;
wallCount = 0;
}
}
}
return list;
}
private int[][] copyGrid(int[][] grid) {
int[][] temp = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
temp[i][j] = grid[i][j];
}
}
return temp;
}
// 每次遍历
// 把temp的当前访问的病毒区域，访问过的设置为2，即将访问的设置为3
// 把grid的当前访问的病毒区域，访问过的设置为2
private void dfs(int[][] temp, int i, int j) {
if (i < 0 || j < 0 || i >= m || j >= n) return;
if (temp[i][j] == 0 || temp[i][j] == 3) wallCount++;
if (temp[i][j] == 0) {
willCount++;
temp[i][j] = 3;
} else if (temp[i][j] == 1) {
temp[i][j] = 2;
grid[i][j] = 2;
for (int k = 0; k < direct.length; k++) {
dfs(temp, i + direct[k][0], j + direct[k][1]);
}
}
}
class Region {
int i;
int j;
int[][] infected; // 感染情况 2: 访问过的病毒区域 3: 未来要变成的病毒区域
int willInfectedCount; // 将要感染的区域的数量
int wallCount; // 需要用的隔离墙的数量
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
# 总结
- 分析出几种情况，然后分别对各个情况实现
