题目

我们从二叉树的根节点 root 开始进行深度优先搜索。

在遍历中的每个节点处，我们输出 D 条短划线（其中 D 是该节点的深度），然后输出该节点的值。（如果节点的深度为 D，则其直接子节点的深度为 D + 1。根节点的深度为 0）。

如果节点只有一个子节点，那么保证该子节点为左子节点。

给出遍历输出 S，还原树并返回其根节点 root。

示例 1：

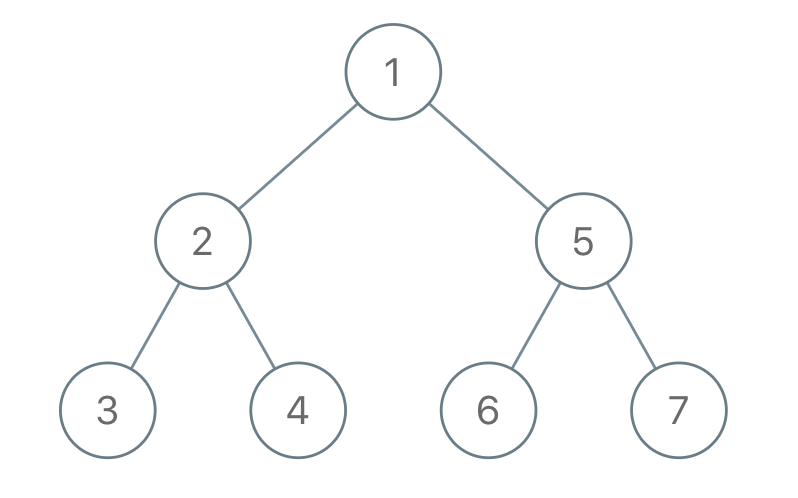
输入："1-2--3--4-5--6--7"
输出：[1,2,5,3,4,6,7]

示例 2：

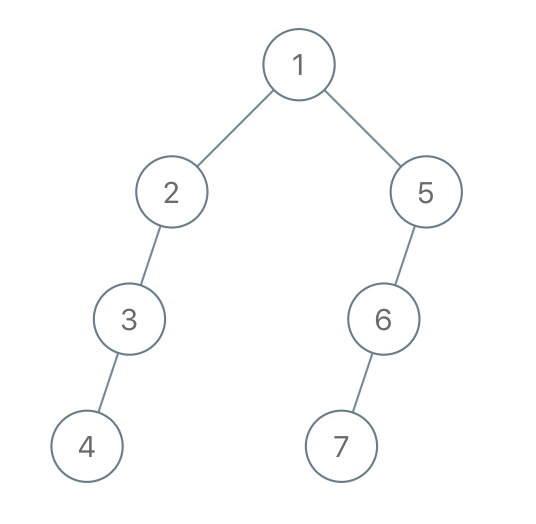
输入："1-2--3---4-5--6---7"
输出：[1,2,5,3,null,6,null,4,null,7]

示例 3：

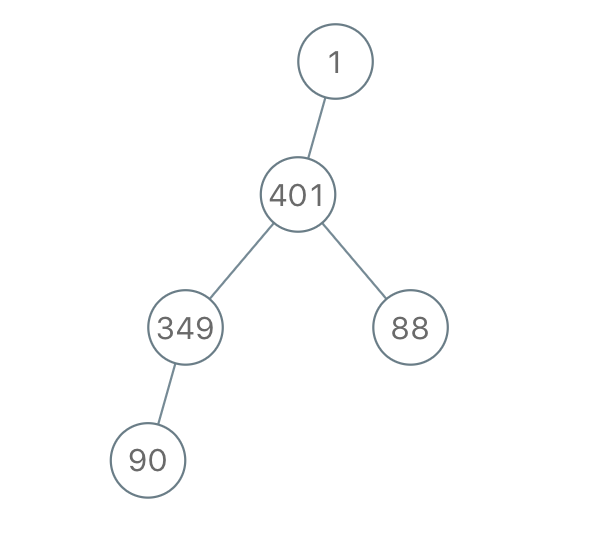
输入："1-401--349---90--88"
输出：[1,401,null,349,88,90]
 

提示：

• 原始树中的节点数介于 1 和 1000 之间。
• 每个节点的值介于 1 和 10 ^ 9 之间。

思路

用LinkedList存储当前节点的路径，往栈中push node节点，最后返回栈中的根节点

解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
     public TreeNode recoverFromPreorder(String S) {
        // 存储当前节点的路径
        Deque<TreeNode> path = new LinkedList<TreeNode>();
        // 存储字符串中的位置
        int pos = 0;
        while (pos < S.length()) {
            // 获取当前层数
            int level = 0;
            while (S.charAt(pos) == '-') {
                ++level;
                ++pos;
            }
            // 获取节点值
            int value = 0;
            while (pos < S.length() && Character.isDigit(S.charAt(pos))) {
                value = value * 10 + (S.charAt(pos) - '0');
                ++pos;
            }
            // 构造当前节点
            TreeNode node = new TreeNode(value);
            if (level == path.size()) {
                //如果当前节点的深度==当前路径长度（前一个节点是当前节点的父节点）
                if (!path.isEmpty()) {
                    //如果不是第一个节点，前一个节点的左子节点为当前节点
                    path.peek().left = node;
                }
            }else {
                //如果当前节点的深度！=当前路径长度（前一个节点不是当前节点的父节点）
                while (level != path.size()) {
                    //通过queue弹出其他子节点，找到当前节点的父节点
                    path.pop();
                }
                // 找到父节点，因为此时左子节点已确定，所以赋值给右子节点
                path.peek().right = node;
            }
            // 放入queue中
            path.push(node);
        }
        // 全部弹出，只剩根节点
        while (path.size() > 1) {
            path.pop();
        }
        // 返回根
        return path.peek();
    }
}