 路径交叉Java
路径交叉Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一个整数数组 distance 。
从 X-Y 平面上的点 (0,0) 开始,先向北移动 distance[0] 米,然后向西移动 distance[1] 米,向南移动 distance[2] 米,向东移动 distance[3] 米,持续移动。也就是说,每次移动后你的方位会发生逆时针变化。
判断你所经过的路径是否相交。如果相交,返回 true ;否则,返回 false 。
示例 1:
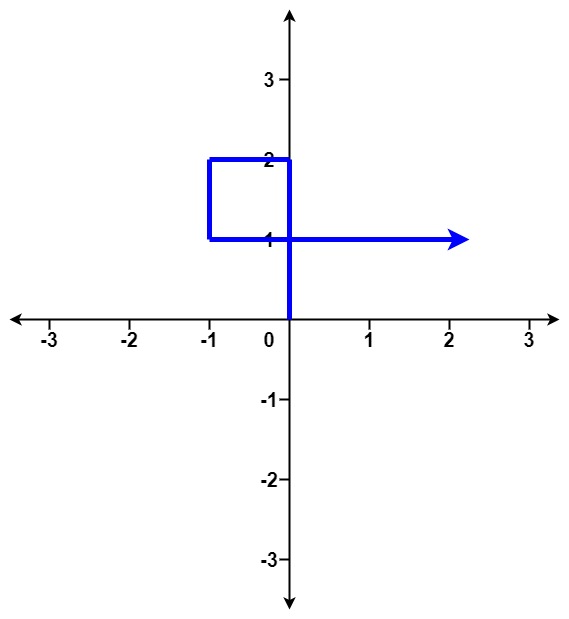
输入:distance = [2,1,1,2]
输出:true
示例 2:
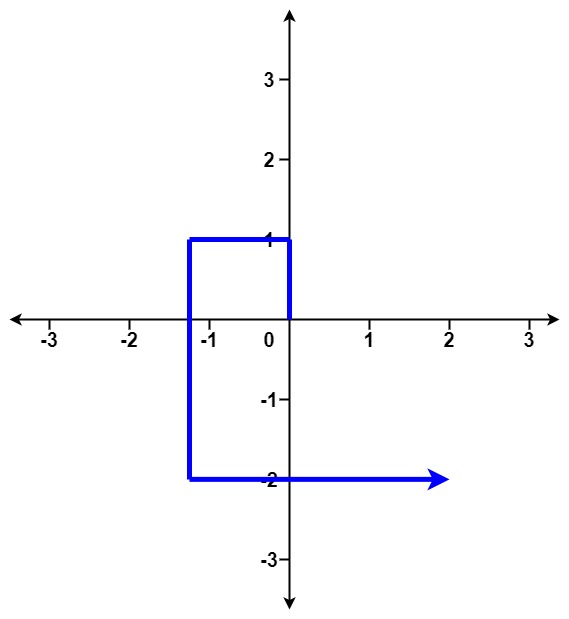
输入:distance = [1,2,3,4]
输出:false
示例 3:
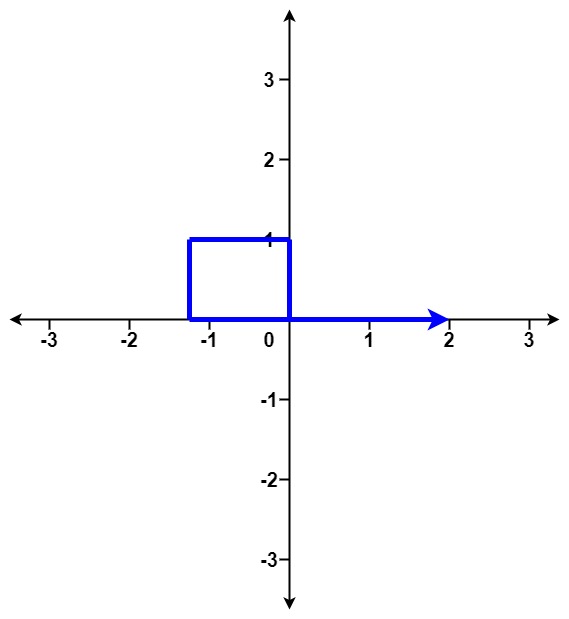
输入:distance = [1,1,1,1]
输出:true
提示:
- 1 <= distance.length <= 105
- 1 <= distance[i] <= 105
# 思路
/**
参考的这篇https://leetcode-cn.com/problems/self-crossing/solution/c3ge-bu-zou-miao-jie-ci-ti-by-xiaohu9527-96n6/
考虑绕圈情况,绕圈有两种:从内向外和从外向内。通过分析可以确定,不相交的只有3种情况:
1. 从distance[0]开始从外向内绕圈,直到结束。
2. 从distance[0]开始从内向外绕圈,直到结束。
3. 从distance[0]开始从内向外绕圈,直到某个时刻开始从外向内绕圈,直到结束。这种情况两次绕圈的最外层不能相交。
从内向外绕圈是distance[i]>distance[i-2],从外向内绕圈则是distance[i]<distance[i-2]。
*/
# 解法
class Solution {
/**
参考的这篇https://leetcode-cn.com/problems/self-crossing/solution/c3ge-bu-zou-miao-jie-ci-ti-by-xiaohu9527-96n6/
考虑绕圈情况,绕圈有两种:从内向外和从外向内。通过分析可以确定,不相交的只有3种情况:
1. 从distance[0]开始从外向内绕圈,直到结束。
2. 从distance[0]开始从内向外绕圈,直到结束。
3. 从distance[0]开始从内向外绕圈,直到某个时刻开始从外向内绕圈,直到结束。这种情况两次绕圈的最外层不能相交。
从内向外绕圈是distance[i]>distance[i-2],从外向内绕圈则是distance[i]<distance[i-2]。
*/
public boolean isSelfCrossing(int[] distance) {
int n = distance.length;
if (n < 4) return false;
int step = 2;
// 第一种情况
if (distance[step] < distance[step-2]){
while (step < n){
if (distance[step] >= distance[step-2]) return true;
++step;
}
return false;
}
// 从distance[0]开始从内向外绕圈
while (step < n){
if (distance[step] <= distance[step-2]) break;
++step;
}
// 第二种情况
if (step >= n) return false;
// 第三种情况
boolean flag1 = distance[step]+(step >= 4 ? distance[step-4] : 0) >= distance[step-2];
boolean flag2 = (step <=n-2 ? distance[step+1] : 0)+(step >= 3 ? distance[step-3] : 0) >= distance[step-1];
if (flag1 && flag2) return true; // 两次绕圈的最外层相交
++step;
while (step < n){
if (distance[step] >= distance[step-2]) return true;
++step;
}
return false;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 总结
- 分析出几种情况,然后分别对各个情况实现


