 奇偶树Java
奇偶树Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
二叉树根节点所在层下标为 0 ,根的子节点所在层下标为 1 ,根的孙节点所在层下标为 2 ,依此类推。
偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
示例 1:
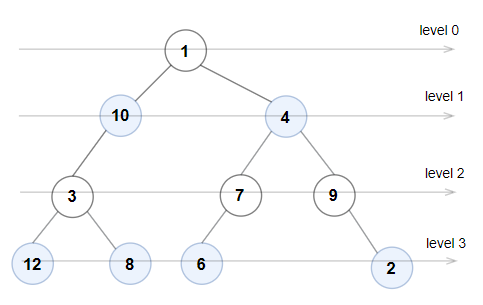
输入:root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
输出:true
解释:每一层的节点值分别是:
0 层:[1]
1 层:[10,4]
2 层:[3,7,9]
3 层:[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
示例 2:
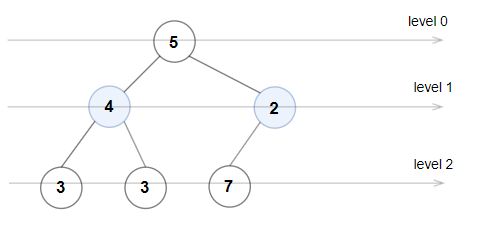
输入:root = [5,4,2,3,3,7]
输出:false
解释:每一层的节点值分别是:
0 层:[5]
1 层:[4,2]
2 层:[3,3,7]
2 层上的节点值不满足严格递增的条件,所以这不是一棵奇偶树。
示例 3:
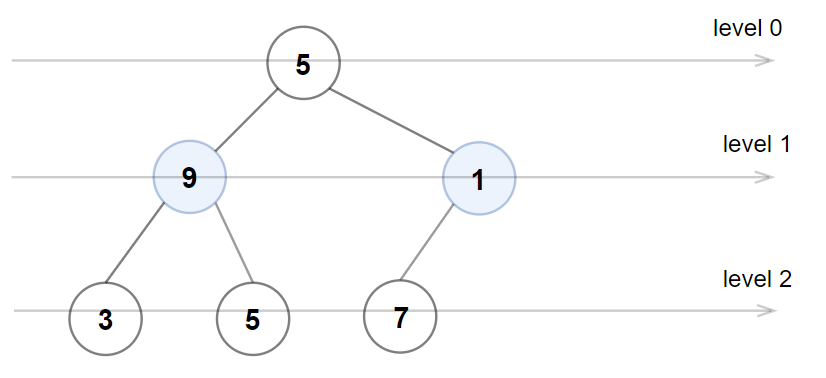
输入:root = [5,9,1,3,5,7]
输出:false
解释:1 层上的节点值应为偶数。
示例 4:
输入:root = [1]
输出:true
示例 5:
输入:root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17]
输出:true
提示:
- 树中节点数在范围 [1, 105] 内
- 1 <= Node.val <= 106
# 思路
Deque
# 解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isEvenOddTree(TreeNode root) {
boolean even = true;
Deque<TreeNode> q = new ArrayDeque<>();
q.offerLast(root);
while (!q.isEmpty()) {
int prev = even ? 0 : 1000000;
for (int i = 0, n = q.size(); i < n; ++i) {
TreeNode node = q.pollFirst();
if (even && (prev >= node.val || node.val % 2 == 0)) {
return false;
}
if (!even && (prev <= node.val || node.val % 2 == 1)) {
return false;
}
prev = node.val;
if (node.left != null) {
q.offerLast(node.left);
}
if (node.right != null) {
q.offerLast(node.right);
}
}
even = !even;
}
return true;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 总结
- 分析出几种情况,然后分别对各个情况实现


