题目

我们正在玩一个猜数游戏，游戏规则如下：

• 我从 1 到 n 之间选择一个数字。
• 你来猜我选了哪个数字。
• 如果你猜到正确的数字，就会 赢得游戏 。
• 如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
• 每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。

给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数，不管我选择那个数字 。

示例 1：

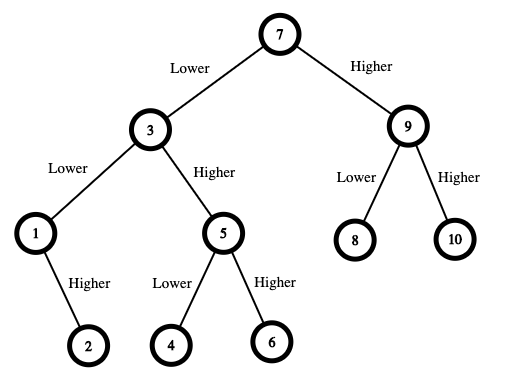
输入：n = 10
输出：16
解释：制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
        - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
        - 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
        - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
            - 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
            - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
        - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
            - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

示例 2：

输入：n = 1
输出：0
解释：只有一个可能的数字，所以你可以直接猜 1 并赢得游戏，无需支付任何费用。

示例 3：

输入：n = 2
输出：1
解释：有两个可能的数字 1 和 2 。
- 你可以先猜 1 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $1 。
    - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $1 。
最糟糕的情况下，你需要支付 $1 。

提示：

• 1 <= n <= 200

思路

    /**
    dp[i][j]表示从[i,j]中猜出正确数字所需要的最少花费金额.(dp[i][i] = 0)
    假设在范围[i,j]中选择x, 则选择x的最少花费金额为: max(dp[i][x-1], dp[x+1][j]) + x
    用max的原因是我们要计算最坏反馈情况下的最少花费金额(选了x之后, 正确数字落在花费更高的那侧)
    
    初始化为(n+2)*(n+2)数组的原因: 处理边界情况更加容易, 例如对于求解dp[1][n]时x如果等于1, 需要考虑dp[0][1](0不可能出现, dp[0][n]为0)
    而当x等于n时, 需要考虑dp[n+1][n+1](n+1也不可能出现, dp[n+1][n+1]为0)
    
    如何写出相应的代码更新dp矩阵, 递推式dp[i][j] = max(max(dp[i][x-1], dp[x+1][j]) + x), x~[i:j], 可以画出矩阵图协助理解, 可以发现
    dp[i][x-1]始终在dp[i][j]的左部, dp[x+1][j]始终在dp[i][j]的下部, 所以更新dp矩阵时i的次序应当遵循bottom到top的规则, j则相反, 由于
    i肯定小于等于j, 所以我们只需要遍历更新矩阵的一半即可(下半矩阵)
    **/

解法

class Solution {
    public int getMoneyAmount(int n) {
        /**
        dp[i][j]表示从[i,j]中猜出正确数字所需要的最少花费金额.(dp[i][i] = 0)
        假设在范围[i,j]中选择x, 则选择x的最少花费金额为: max(dp[i][x-1], dp[x+1][j]) + x
        用max的原因是我们要计算最坏反馈情况下的最少花费金额(选了x之后, 正确数字落在花费更高的那侧)
        
        初始化为(n+2)*(n+2)数组的原因: 处理边界情况更加容易, 例如对于求解dp[1][n]时x如果等于1, 需要考虑dp[0][1](0不可能出现, dp[0][n]为0)
        而当x等于n时, 需要考虑dp[n+1][n+1](n+1也不可能出现, dp[n+1][n+1]为0)
        
        如何写出相应的代码更新dp矩阵, 递推式dp[i][j] = max(max(dp[i][x-1], dp[x+1][j]) + x), x~[i:j], 可以画出矩阵图协助理解, 可以发现
        dp[i][x-1]始终在dp[i][j]的左部, dp[x+1][j]始终在dp[i][j]的下部, 所以更新dp矩阵时i的次序应当遵循bottom到top的规则, j则相反, 由于
        i肯定小于等于j, 所以我们只需要遍历更新矩阵的一半即可(下半矩阵)
        **/
        int[][] dp = new int[n+2][n+2];
        for(int i = n; i >= 1; --i) {
            for(int j = i; j <= n; ++j) {
                if(i == j)
                    dp[i][j] = 0;
                else {
                    dp[i][j] = Integer.MAX_VALUE;
                    for(int x = i; x <= j; ++x) 
                        dp[i][j] = Math.min(dp[i][j], Math.max(dp[i][x-1], dp[x+1][j]) + x);
                }
            }
        }
        return dp[1][n];

    }
}

总结

• 分析出几种情况，然后分别对各个情况实现