题目

给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。

这里，平面上两点之间的距离是 欧几里德距离（ √(x1 - x2)² + (y1 - y2)² ）。

你可以按 任何顺序 返回答案。除了点坐标的顺序之外，答案 确保 是 唯一 的。

示例 1：

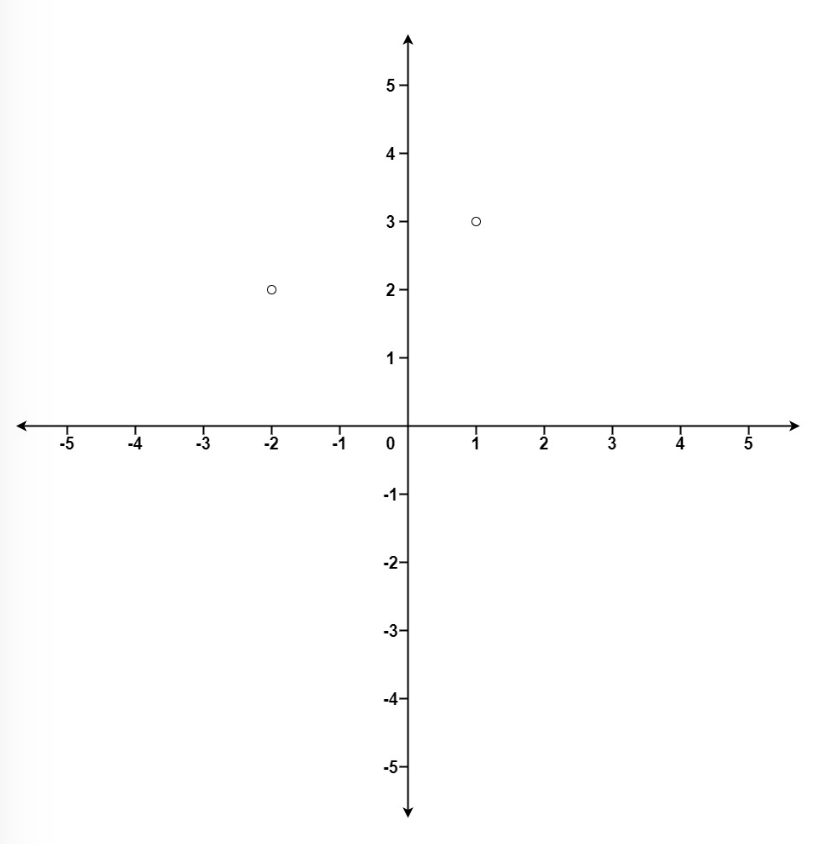
输入：points = [[1,3],[-2,2]], k = 1
输出：[[-2,2]]
解释： 
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。

示例 2：

输入：points = [[3,3],[5,-1],[-2,4]], k = 2
输出：[[3,3],[-2,4]]
（答案 [[-2,4],[3,3]] 也会被接受。）

提示：

• 1 <= k <= points.length <= 10⁴
• -10⁴ < xi, yi < 10⁴

思路

小顶堆

解法

class Solution {
    public int[][] kClosest(int[][] points, int k) {
        //(x-0)^2+(y-0)^2
        PriorityQueue<int[]> minHeap = new PriorityQueue<>((a,b)->(a[0]*a[0]+a[1]*a[1]-b[0]*b[0]-b[1]*b[1]));  //小顶堆
        for(int[] point : points){
            minHeap.offer(point);
        }
        int[][] res = new int[k][2];
        for(int i=0;i<k;i++){  //取出前k个距离原点最近的点
            res[i][0]=minHeap.peek()[0];
            res[i][1]=minHeap.poll()[1];
        }
        return res;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现