题目

给你二叉树的根结点 root ，请你设计算法计算二叉树的 垂序遍历 序列。

对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。

二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束，按列索引每一列上的所有结点，形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点，则按结点的值从小到大进行排序。

返回二叉树的 垂序遍历 序列。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[9],[3,15],[20],[7]]
解释：
列 -1 ：只有结点 9 在此列中。
列  0 ：只有结点 3 和 15 在此列中，按从上到下顺序。
列  1 ：只有结点 20 在此列中。
列  2 ：只有结点 7 在此列中。

示例 2：

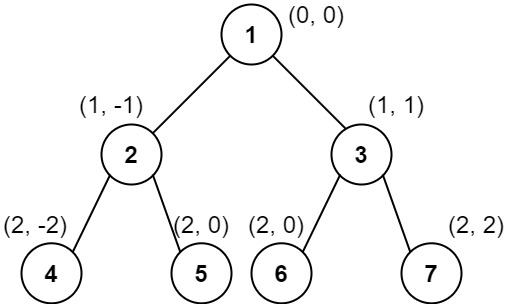
输入：root = [1,2,3,4,5,6,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
列 -2 ：只有结点 4 在此列中。
列 -1 ：只有结点 2 在此列中。
列  0 ：结点 1 、5 和 6 都在此列中。
          1 在上面，所以它出现在前面。
          5 和 6 位置都是 (2, 0) ，所以按值从小到大排序，5 在 6 的前面。
列  1 ：只有结点 3 在此列中。
列  2 ：只有结点 7 在此列中。

示例 3：

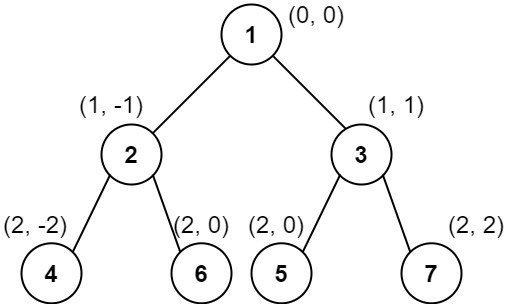
输入：root = [1,2,3,4,6,5,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
这个示例实际上与示例 2 完全相同，只是结点 5 和 6 在树中的位置发生了交换。
因为 5 和 6 的位置仍然相同，所以答案保持不变，仍然按值从小到大排序。
 

提示：

• 树中结点数目总数在范围 [1, 1000] 内
• 0 <= Node.val <= 1000

思路

定义节点Tuple{x,y,val},设置dfs遍历node，并把结果存在list中，最后对list中元素排序返回结果

解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Tuple> list;
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        list = new ArrayList<>();
        dfs(root,0,0);

        list.sort((t1,t2)->{
            int num1 = t1.y-t2.y;
            int num2 = num1==0? t1.x-t2.x:num1;
            int num3 = num2==0? t1.val-t2.val:num2;
            return num3;
        });

        List<List<Integer>> res = new ArrayList<>();
        int last = Integer.MIN_VALUE;
        for(Tuple tuple:list){
            if(tuple.y!=last){
                last = tuple.y;
                List<Integer> temp = new ArrayList<>();
                temp.add(tuple.val);
                res.add(temp);
            }
            else{
                res.get(res.size()-1).add(tuple.val);
            }
        }
        return res;

    }

    public void dfs(TreeNode root,int x,int y){
        if(root == null) return;
        dfs(root.left,x+1,y-1);
        list.add(new Tuple(root.val,x,y));
        dfs(root.right,x+1,y+1);
    }

    public class Tuple{
        int val;
        int x;
        int y;
        public Tuple(int val,int x,int y){
            this.val = val;
            this.x = x;
            this.y = y;
        }
    }
}