 细分图中的可到达节点Java
细分图中的可到达节点Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一个无向图(原始图),图中有 n 个节点,编号从 0 到 n - 1 。你决定将图中的每条边 细分 为一条节点链,每条边之间的新节点数各不相同。
图用由边组成的二维数组 edges 表示,其中 edges[i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi 之间存在一条边,cnti 是将边 细分 后的新节点总数。注意,cnti == 0 表示边不可细分。
要 细分 边 [ui, vi] ,需要将其替换为 (cnti + 1) 条新边,和 cnti 个新节点。新节点为 x1, x2, ..., xcnti ,新边为 [ui, x1], [x1, x2], [x2, x3], ..., [xcnti-1, xcnti], [xcnti, vi] 。
现在得到一个 新的细分图 ,请你计算从节点 0 出发,可以到达多少个节点?如果节点间距离是 maxMoves 或更少,则视为 可以到达 。
给你原始图和 maxMoves ,返回 新的细分图中从节点 0 出发 可到达的节点数 。
示例 1:
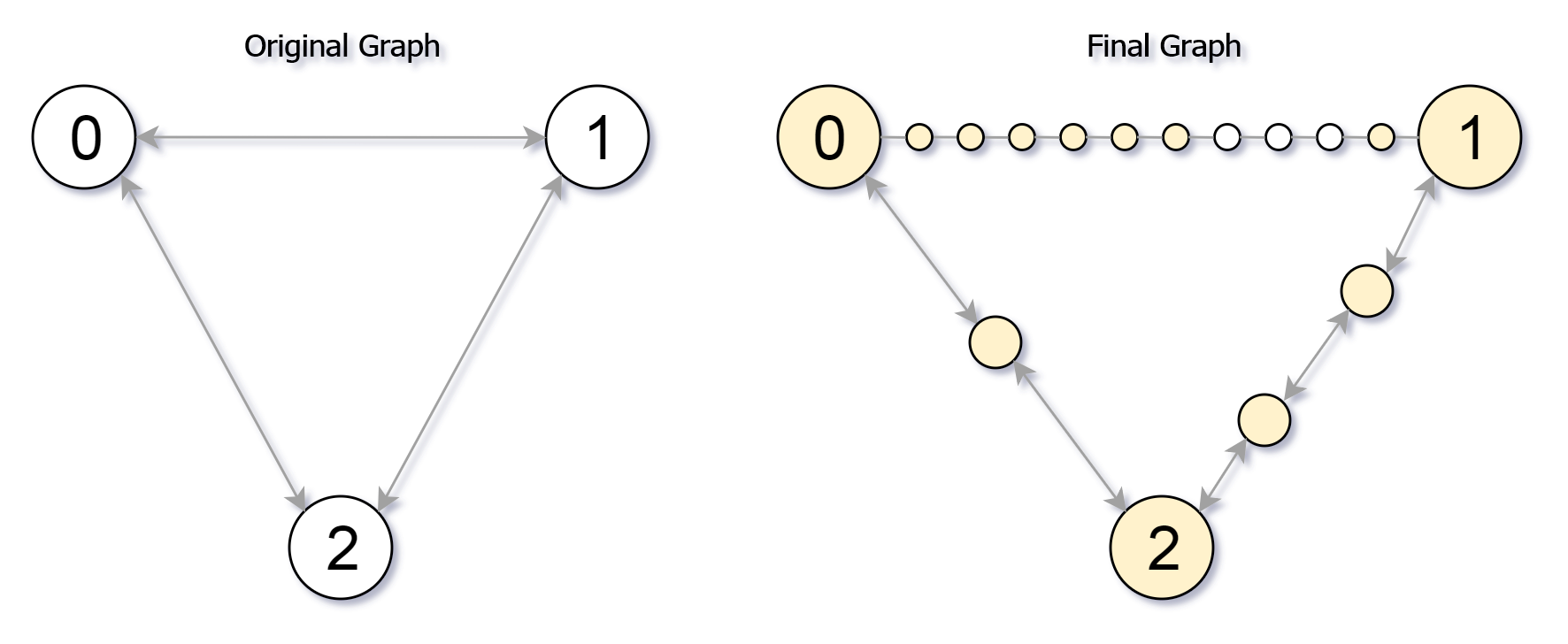 输入:edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出:13
解释:边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。
示例 2:
输入:edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出:13
解释:边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。
示例 2:
输入:edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
输出:23
示例 3:
输入:edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
输出:1
解释:节点 0 与图的其余部分没有连通,所以只有节点 0 可以到达。
提示:
- 0 <= edges.length <= min(n * (n - 1) / 2, 104)
- edges[i].length == 3
- 0 <= ui < vi < n
- 图中 不存在平行边
- 0 <= cnti <= 104
- 0 <= maxMoves <= 109
- 1 <= n <= 3000
# 思路
dist[]可以看作原点到每个大点最多剩余多少步,小点可以根据这个直接更新
# 解法
class Solution {
public int reachableNodes(int[][] edges, int maxMoves, int n) {
List<int[]>[] g = new List[n];
for (int i = 0; i < n; i++) {
g[i] = new ArrayList<>();
}
for (int[] edge : edges) {
g[edge[0]].add(new int[]{edge[1], edge[2]});
g[edge[1]].add(new int[]{edge[0], edge[2]});
}
PriorityQueue<int[]> queue = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o2[1] - o1[1];
}
});
queue.add(new int[]{0, maxMoves});
// 代表0到该位置,最多剩多少步
int[] dist = new int[n];
Arrays.fill(dist, 0);
dist[0] = maxMoves;
boolean[] visited = new boolean[n];
int ret = 0;
while (!queue.isEmpty()) {
int[] poll = queue.poll();
int x = poll[0], left = poll[1];
if (visited[x] || dist[x] > left) {
continue;
}
visited[x] = true;
ret++;
List<int[]> _edges = g[x];
if (_edges.size() == 0) {
continue;
}
for (int[] edge : _edges) {
// update distance
if (dist[x] > edge[1]) {
int max = Math.max(dist[x] - edge[1] - 1, dist[edge[0]]);
dist[edge[0]] = max;
queue.add(new int[]{edge[0], max});
}
}
}
// sum all small nodes
for (int[] edge : edges) {
ret += Math.min(dist[edge[0]] + dist[edge[1]], edge[2]);
}
return ret;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# 总结
- 分析出几种情况,然后分别对各个情况实现


