题目

给你一个 m x n 的矩阵 M ，初始化时所有的 0 和一个操作数组 op ，其中 ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

示例 1:

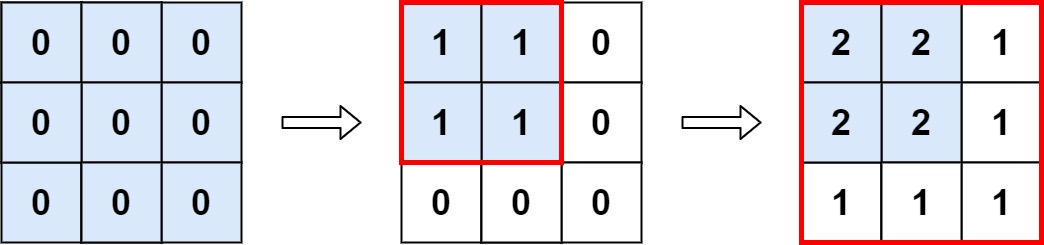
输入: m = 3, n = 3，ops = [[2,2],[3,3]] 输出: 4 解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。 示例 2:

输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4

示例 3:

输入: m = 3, n = 3, ops = []
输出: 9

提示:

• 1 <= m, n <= 4 * 10⁴
• 0 <= ops.length <= 10⁴
• ops[i].length == 2
• 1 <= ai <= m
• 1 <= bi <= n

思路

Math.min

解法

class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        if(ops.length==0){
            return m*n;
        }
        int a=Integer.MAX_VALUE;
        int b=Integer.MAX_VALUE;
        for(int i=0;i<ops.length;i++){
            a=Math.min(a,ops[i][0]);
            b=Math.min(b,ops[i][1]);
        }
        return a*b;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现