连接所有点的最小费用Java

文章发布较早，内容可能过时，阅读注意甄别。

# 题目

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的曼哈顿距离：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间有且仅有一条简单路径时，才认为所有点都已连接。

示例 1：

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20

解释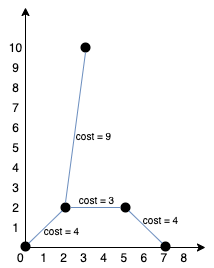：我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。注意到任意两个点之间只有唯一一条路径互相到达。示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

示例 5：

输入：points = [[0,0]]
输出：0

提示：

1 <= points.length <= 1000
-106 <= xi, yi <= 10⁶
所有点 (xi, yi) 两两不同。

# 思路

union

# 解法

class Solution {
    public int minCostConnectPoints(int[][] points) {
        //MST问题 Kruskal求解
        int n = points.length;
        int rows = points.length;
        int cols = points.length;
        UnionFind uf = new UnionFind(n);

        PriorityQueue<int[]> pq = new PriorityQueue<>(
            (a,b) -> a[2] - b[2]
        );//优先级队列，保存边集，按权值从小到达排序

        //保存所有边权值
        for(int i = 0; i < rows; i++) {
            int[] a = points[i];
            for(int j = i + 1; j < cols; j++) {
                int[] b = points[j];
                int value = Math.abs(a[0] - b[0]) + Math.abs(a[1] - b[1]);
                pq.offer(new int[]{i, j, value});
            }
        }

        int res = 0;
        while (uf.getCount() > 1) {
            int[] edge = pq.poll();//每次取出最小权值的边，加入到点集中
            int a = edge[0];
            int b = edge[1];
            int value = edge[2];
            if(uf.union(a, b)) {//能加入，计算总权值，不能加入，选择下一条边
                res += value;
            }
        }

        return res;
    }

    class UnionFind {
        int[] parent;
        int[] rank;
        int count;

        public UnionFind (int n) {
            parent = new int[n];
            rank = new int[n];
            count = n;
            for(int i = 0; i < n; i++) {
                parent[i] = i;
                rank[i] = 0;
            }
        }

        public int find (int i) {
            if(i != parent[i]) {
                parent[i] = find(parent[i]);
            }
            return parent[i];
        }

        public boolean union (int i, int j) {
            int rootI = find(i);
            int rootJ = find(j);
            if(rootI != rootJ) {
                if(rank[rootI] < rank[rootJ]) {
                    parent[rootI] = rootJ;
                } else if(rank[rootI] > rank[rootJ]) {
                    parent[rootJ] = rootI;
                } else {
                    parent[rootI] = rootJ;
                    rank[rootJ]++;
                }
                count--;
                return true;
            }
            return false;
        }

        public int getCount () {
            return count;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

# 总结

分析出几种情况，然后分别对各个情况实现

#Java