 找到最终的安全状态Java
找到最终的安全状态Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
有一个有 n 个节点的有向图,节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示, graph[i]是与节点 i 相邻的节点的整数数组,这意味着从节点 i 到 graph[i]中的每个节点都有一条边。
如果一个节点没有连出的有向边,则它是 终端节点 。如果没有出边,则节点为终端节点。如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。
示例 1:
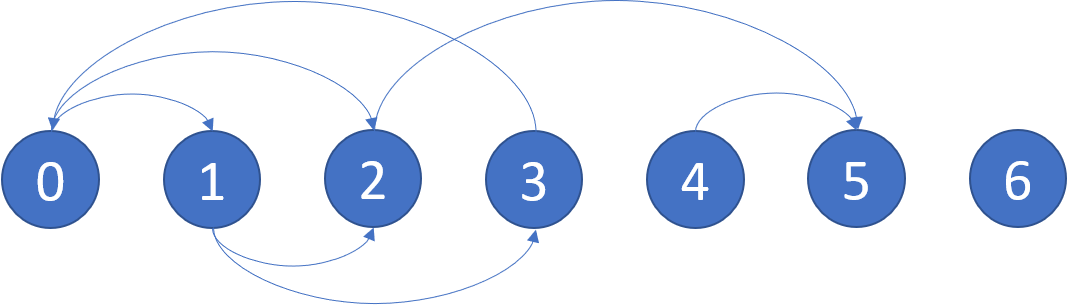
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出:[2,4,5,6]
解释:示意图如上。
节点 5 和节点 6 是终端节点,因为它们都没有出边。
从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出:[4]
解释:
只有节点 4 是终端节点,从节点 4 开始的所有路径都通向节点 4 。
提示:
- n == graph.length
- 1 <= n <= 104
- 0 <= graph[i].length <= n
- 0 <= graph[i][j] <= n - 1
- graph[i] 按严格递增顺序排列。
- 图中可能包含自环。
- 图中边的数目在范围 [1, 4 * 104] 内。
# 思路
记忆化dfs
# 解法
class Solution {
// 记忆化dfs
public List<Integer> eventualSafeNodes(int[][] graph) {
int[] mem = new int[graph.length]; //记忆化dfs关键,存储点的状态,0未访问,1安全点,2非安全点;
boolean[] visited = new boolean[graph.length]; //单次dfs遍历中判断点是否访问过
for (int i = 0; i < graph.length; i++) {
dfs(graph, mem, visited, i);
}
List<Integer> res = new ArrayList<>();
for (int i = 0; i < mem.length; i++) {
if (mem[i] == 1) res.add(i);
}
return res;
}
boolean dfs (int[][] map, int[] mem, boolean[] visited, int start) {
if (mem[start] != 0) {
return mem[start] == 1 ? true : false;
}
boolean res = true;
for (int i : map[start]) {
if (visited[i]) {
return false;
}
visited[i] = true;
res = res && dfs(map, mem, visited, i); //从当前节点出发所有点都是安全的则为安全,否则为不安全;
visited[i] = false;
if (!res) break;
}
mem[start] = res ? 1 : 2;
return res;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 总结
- 分析出几种情况,然后分别对各个情况实现


