可以攻击国王的皇后Java

文章发布较早，内容可能过时，阅读注意甄别。

# 题目

在一个 8x8 的棋盘上，放置着若干「黑皇后」和一个「白国王」。

给定一个由整数坐标组成的数组 queens ，表示黑皇后的位置；以及一对坐标 king ，表示白国王的位置，返回所有可以攻击国王的皇后的坐标(任意顺序)。

示例 1：

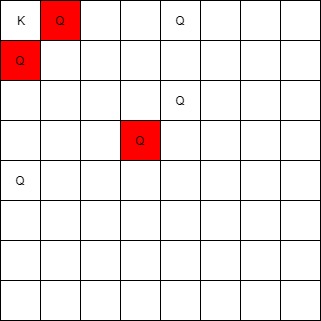
输入：queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出：[[0,1],[1,0],[3,3]]
解释： 
[0,1] 的皇后可以攻击到国王，因为他们在同一行上。 
[1,0] 的皇后可以攻击到国王，因为他们在同一列上。 
[3,3] 的皇后可以攻击到国王，因为他们在同一条对角线上。 
[0,4] 的皇后无法攻击到国王，因为她被位于 [0,1] 的皇后挡住了。 
[4,0] 的皇后无法攻击到国王，因为她被位于 [1,0] 的皇后挡住了。 
[2,4] 的皇后无法攻击到国王，因为她和国王不在同一行/列/对角线上。

示例 2：

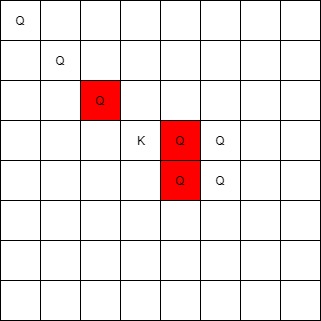
输入：queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出：[[2,2],[3,4],[4,4]]

示例 3：

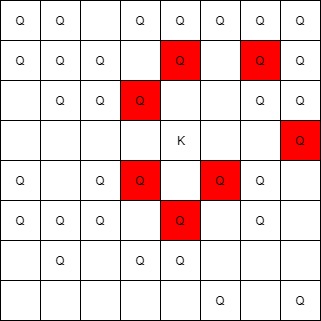
输入：queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
输出：[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

提示：

1 <= queens.length <= 63
queens[i].length == 2
0 <= queens[i][j] < 8
king.length == 2
0 <= king[0], king[1] < 8
一个棋盘格上最多只能放置一枚棋子。

# 思路

/**

使用seen数组判断棋盘该位置是否有queen，有为true,没有为false
遍历king的所有方向，并移动，如果遇到queen,则将该位置加入到结果中，并break跳出循环，说明该方向已找到，不用再继续找了 */

# 解法


class Solution {
/**
1. 使用seen数组判断棋盘该位置是否有queen，有为true,没有为false
2. 遍历king的所有方向，并移动，如果遇到queen,则将该位置加入到结果中，并break跳出循环，说明该方向已找到，
    不用再继续找了
 */
    public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
        List<List<Integer>>result = new ArrayList<>();
        boolean[][]seen = new boolean[8][8];
        for(int[] queen:queens){
            seen[queen[0]][queen[1]]=true;
        }
        int[] directions = new int[]{-1,0,1};
        for(int dx: directions){
            for(int dy: directions){
                if(dx==0&&dy==0)continue;
                int x = king[0];
                int y = king[1];
                while(x+dx>=0 && x+dx<8 && y+dy>=0&&y+dy<8){
                    x = x+dx;
                    y = y+dy;
                    if(seen[x][y]){
                        result.add(Arrays.asList(x,y));
                        break;
                    }
                }
            }
        }
        return result;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 总结

分析出几种情况，然后分别对各个情况实现