 路径总和IIIJava
路径总和IIIJava
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
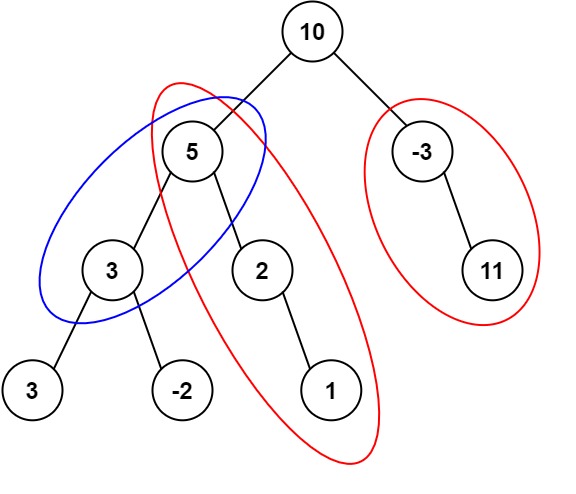
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
提示:
- 二叉树的节点个数的范围是 [0,1000]
- -109 <= Node.val <= 109
- -1000 <= targetSum <= 1000
# 思路
前缀和,先序遍历
# 解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int ans;
public int pathSum(TreeNode root, int targetSum) {
Map<Long, Integer> prefix = new HashMap<>();
//当targetSum 等于某个节点值时,curPrefix - targetSum = 0,当前节点自己就算做一条符合条件的路径,所以也要计数
prefix.put(0L, 1);
dfs(root, prefix, 0L, targetSum);
return ans;
}
//先序遍历
private void dfs (TreeNode root, Map<Long, Integer> prefix, long curPrefix, int targetSum) {
//递归终止的条件
if (root == null) {
return;
}
//当前节点的前缀和
curPrefix += root.val;
//查看是否有curPrefix - targetSum的前缀和已经存在
int cnt = prefix.getOrDefault(curPrefix - targetSum, 0);
ans += cnt;
//记录前缀和
prefix.put(curPrefix, prefix.getOrDefault(curPrefix, 0) + 1);
//遍历左子树
dfs(root.left, prefix, curPrefix, targetSum);
//遍历右子树
dfs(root.right, prefix, curPrefix, targetSum);
//因为先序遍历是遍历根、左、右,即当前节点及其所有子节点,所以当遍历完当前节点和其所有子节点之后,当前节点的前缀和就没有用了,就需要把map里的记录删除,否则会影响其他子树的计算。跟当前节点没有路径关系的节点,不需要当前节点的前缀和
prefix.put(curPrefix, prefix.getOrDefault(curPrefix, 0) - 1);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


