题目

给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

示例 1:

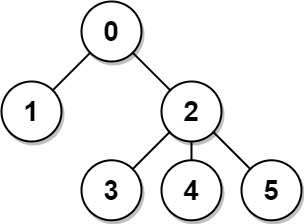
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

示例 2:

输入: n = 1, edges = []
输出: [0]

示例 3:

输入: n = 2, edges = [[1,0]]
输出: [1,1]

提示:

• 1 <= n <= 3 * 10⁴
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 给定的输入保证为有效的树

思路

dfs

解法

class Solution {
    
    public int[] sumOfDistancesInTree(int N, int[][] edges) {
        int[] result = new int[N];//最终结果存放处
        ArrayList<Node> nodeList = new ArrayList<Node>(N);
        for (int i = 0; i < N; i++) {
            nodeList.add(new Node(i));
        }
        for (int i = 0; i < edges.length; i++) {
            int a = edges[i][0];
            int b = edges[i][1];
            Node nodeA = nodeList.get(a);
            Node nodeB = nodeList.get(b);
            nodeA.link(nodeB);
        }
        Node root = nodeList.get(0);
        root.traverse();//建立以0节点为根节点的一棵树
        root.initiate();//计算0节点的各种距离 递归先算子树距离
        root.totalDistance = root.subDistance; 
        root.calculateDistance(N);//换根 用状态转移公式 dfs遍历
        //存储结果：
        for (int i = 0; i < N; i++) {
            result[i] = nodeList.get(i).totalDistance;
        }
        return result;
    }

    class Node {
        int val;
        Node parent;//父节点
        List<Node> nodes;//邻接节点
        int size;//以nodes为根的树有多少节点（包括本身）
        boolean visited;
        int subDistance;
        int totalDistance;
        public Node(int val) {
            this.val = val;
            this.parent = null;
            this.nodes = new ArrayList<Node>();
            this.size = 1;
            this.visited = false;
            this.subDistance = 0; //以该节点为子树包含的距离
            this.totalDistance = 0; //该节点的最终结果
            // 对于0节点 两个距离最后计算完了会相等
            // 对于0以外的节点 totalDistance都是通过其他节点的totalDistance进行状态转换得来的
            // 0以外的节点，totalDistance和subDistance不同
        }

        // 将本节点与anotherNode节点连接起来 
        // 连接是双向的 即同时建立两条无向边
        public void link(Node anotherNode) {
            this.nodes.add(anotherNode);
            anotherNode.nodes.add(this);
        }

        // 从node开始 dfs遍历
        // 一边遍历一边移除根节点 防止遍历的时候返回去
        public void traverse() {
            for (Node node: nodes) {
                node.parent = this; //邻接节点的父节点指向当前节点 表示是从当前节点来的
                node.nodes.remove(this);// 一边遍历一边移除根节点 防止遍历的时候返回去
                node.traverse(); //dfs递归
            }
        }

        // 遍历统计子树的信息
        public void initiate() {
            for (Node node: nodes) {
                node.initiate();
                this.size += node.size; //更新节点数=已有节点数+子树节点数
                this.subDistance += node.subDistance;//更新距离=已有距离+子树距离
                this.subDistance += node.size;//更新距离=已有距离+子树节点数
                // 因为每一个子树节点连接到当前节点还要再多一条线
            }
        }

        // 状态转移 对邻接节点换根 dfs遍历
        public void calculateDistance(int N) {
            // 遍历时并不会遍历到本节点的根节点 这个问题已经在traverse()里面解决了
            for (Node node: nodes) {
                // 状态转移方程 计算node节点的最终结果
                node.totalDistance = this.totalDistance + N - node.size * 2;
                // dfs遍历node的邻接节点
                node.calculateDistance(N);
            }
        }
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现