1727. 重新排列后的最大子矩阵Java
文章发布较早，内容可能过时，阅读注意甄别。
# 题目
给你一个二进制矩阵 matrix ，它的大小为 m x n ，你可以将 matrix 中的 列 按任意顺序重新排列。
请你返回最优方案下将 matrix 重新排列后，全是 1 的子矩阵面积。
示例 1：
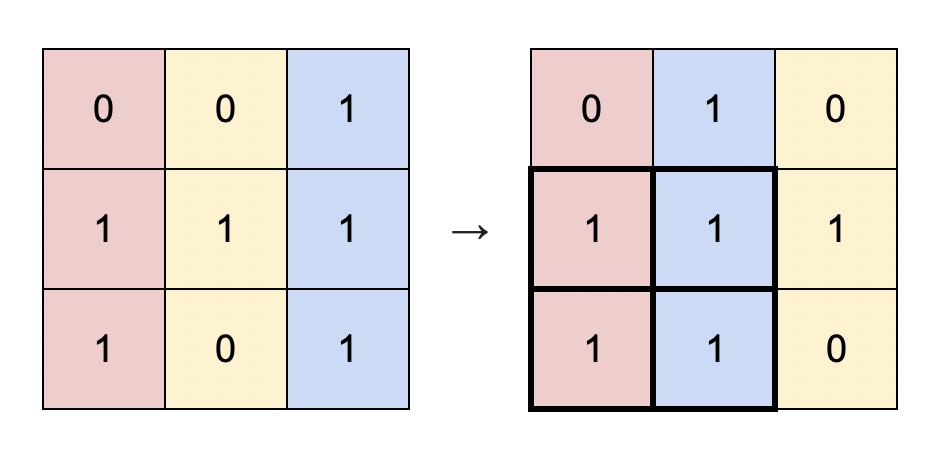
输入：matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出：4
解释：你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分，面积为 4 。
示例 2：
输入：matrix = [[1,0,1,0,1]]
输出：3
解释：你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分，面积为 3 。
示例 3：
输入：matrix = [[1,1,0],[1,0,1]]
输出：2
解释：由于你只能整列整列重新排布，所以没有比面积为 2 更大的全 1 子矩形。
示例 4：
输入：matrix = [[0,0],[0,0]]
输出：0
解释：由于矩阵中没有 1 ，没有任何全 1 的子矩阵，所以面积为 0 。
提示：
- m == matrix.length
- n == matrix[i].length
- 1 <= m * n <= 105
- matrix[i][j] 要么是 0 ，要么是 1 。
# 思路
数组记录连续1的个数
# 解法
class Solution {
public int largestSubmatrix(int[][] matrix) {
int res = 0;
int m = matrix.length, n= matrix[0].length;
int[] heights = new int[n];
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
//用来记录当前行以及以上行的每列连续1的个数
heights[j] = matrix[i][j] == 0 ? 0 : heights[j] + 1;
}
//防止对heights数组污染
int[] temp = heights.clone();
Arrays.sort(temp);
//枚举每个高度的矩形并取最大值
for(int j = 0; j < n; j++)
res = Math.max(res, temp[j] * (n - j));
}
return res;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 总结
- 分析出几种情况，然后分别对各个情况实现
