 矩形面积Java
矩形面积Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。
每个矩形由其 左下 顶点和 右上 顶点坐标表示:
- 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
- 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。
示例 1:
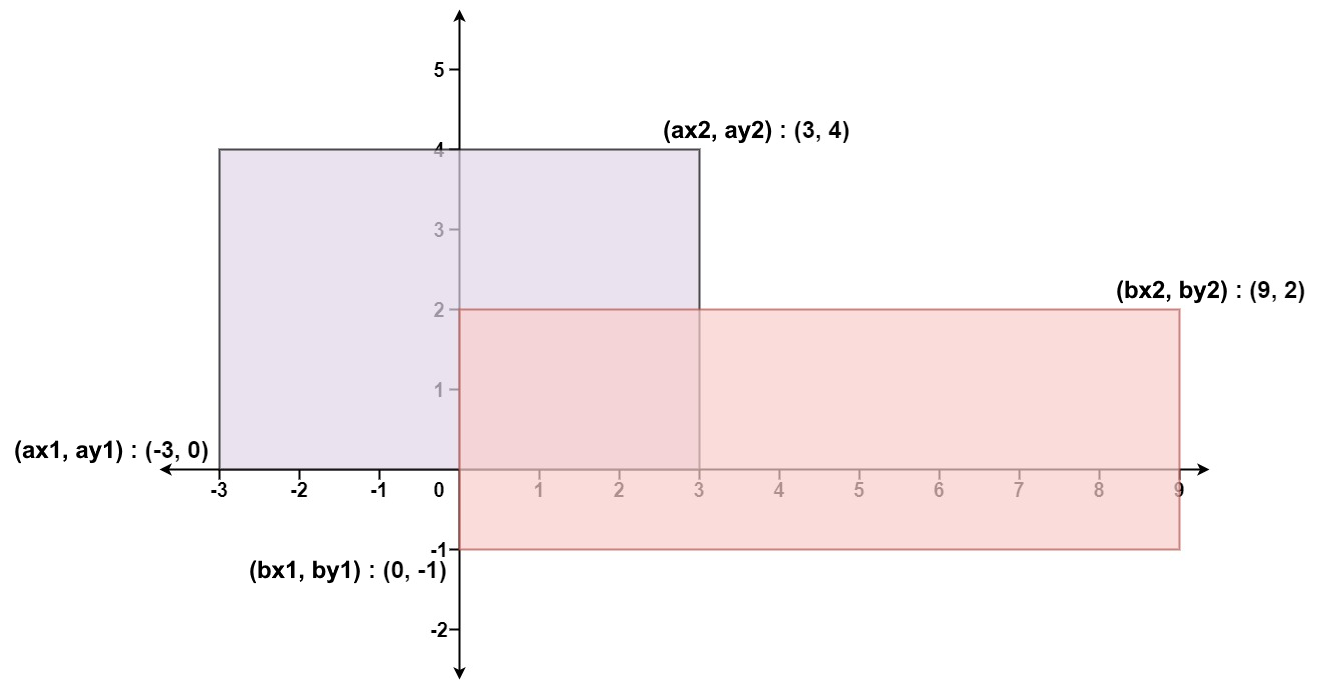
输入:ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出:45
示例 2:
输入:ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出:16
提示:
-104 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 10<sup>4</sup>
# 思路
【笔记】总面积=单个面积1+单个面积2-重叠面积。
但是,我们应该写成:(先做减法)
总面积 = 单个面积1 - 重叠面积 + 单个面积2
这样,才不会溢出。
1
2
2
假设左边是 a, 右边是 b
┌--------┓
| |
| ┌---╋-----┓
| | | |
┗----╋---┘ |
| |
┗---------┘
┗、┓是已知的坐标
求两个 ╋ 的坐标就好啦
左下角: [x1, y1] = [max(ax1, bx1), max(ay1, ay2)]
右上角: [x2, y2] = [min(ax2, bx2), min(ay2, by2)]
所以, 重叠部分面积就是 (x2 - x1) * (y2 - y1)
当然, 这是假设有重叠部分的前提下得出的结论
如若没有重叠部分, 如下:
┌--------┓
| |
| | ┌---------┓
| | | |
┗--------┘ | |
| |
┗---------┘
那么 x1 = bx1, x2 = ax2 (用上述方式), 即 x2 - x1 < 0
所以严谨的说, 重叠部分面积应该是:
max(0, x2 - x1) * max(0, y2 - y1)
# 解法
class Solution {
public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
int x1=Math.max(ax1,bx1);
int y1=Math.max(ay1,by1);
int x2=Math.min(ax2,bx2);
int y2=Math.min(ay2,by2);
if(x1>=x2||y1>=y2)
return ((ax2-ax1)*(ay2-ay1)+(bx2-bx1)*(by2-by1));
else
return ((ax2-ax1)*(ay2-ay1)-(x2-x1)*(y2-y1)+(bx2-bx1)*(by2-by1));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 总结
- 分析出几种情况,然后分别对各个情况实现


