 生命游戏Java
生命游戏Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
根据 百度百科 , 生命游戏 ,简称为 生命 ,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态,返回下一个状态。
示例 1:
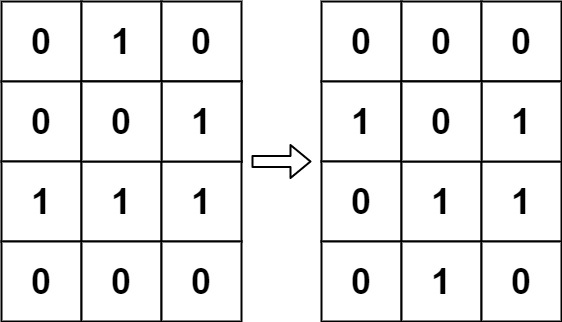
输入:board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
示例 2:
输入:board = [[1,1],[1,0]]
输出:[[1,1],[1,1]]
提示:
- m == board.length
- n == board[i].length
- 1 <= m, n <= 25
- board[i][j] 为 0 或 1
进阶:
- 你可以使用原地算法解决本题吗?请注意,面板上所有格子需要同时被更新:你不能先更新某些格子,然后使用它们的更新后的值再更新其他格子。
- 本题中,我们使用二维数组来表示面板。原则上,面板是无限的,但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题?
# 思路
利用一个 two bits 的状态机来记录细胞状态, 第一位表示
下一状态, 第二位表示当前状态:
00: dead (next state) <- dead (current state)
01: dead (next state) <- live (current state)
10: live (next state) <- dead (current state)
11: live (next state) <- live (current state)
初始情况对应就是 00 和 01 (默认下一状态是 dead state)
统计每个位置周围的 live 细胞数决定高位置 1 (live)还是
0 (dead), 最后右移一位即为最终状态, 注意不需要考虑 01
以及 00 的情况, 因为已经默认下一状态为 dead.
# 解法
class Solution {
public void gameOfLife(int[][] board) {
/**
利用一个 two bits 的状态机来记录细胞状态, 第一位表示
下一状态, 第二位表示当前状态:
00: dead (next state) <- dead (current state)
01: dead (next state) <- live (current state)
10: live (next state) <- dead (current state)
11: live (next state) <- live (current state)
初始情况对应就是 00 和 01 (默认下一状态是 dead state)
统计每个位置周围的 live 细胞数决定高位置 1 (live)还是
0 (dead), 最后右移一位即为最终状态, 注意不需要考虑 01
以及 00 的情况, 因为已经默认下一状态为 dead.
**/
if(board.length < 1) return;
// 更新矩阵
for(int i = 0; i < board.length; ++i) {
for(int j = 0; j < board[0].length; ++j) {
int lives = countLives(board, i, j);
// live -> live
if((board[i][j] & 1) == 1) {
if(lives >= 2 && lives <= 3)
board[i][j] = 3;
}
// dead -> live
else {
if(lives == 3)
board[i][j] = 2;
}
}
}
// 重置矩阵
for(int i = 0; i < board.length; ++i) {
for(int j = 0; j < board[0].length; ++j)
board[i][j] >>= 1;
}
}
private int countLives(int[][] b, int i, int j) {
int count = 0;
int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}};
for(int[] dir : dirs) {
int x = i + dir[0];
int y = j + dir[1];
if(x < 0 || x > b.length-1 || y < 0 || y > b[0].length-1)
continue;
count += (b[x][y] & 1);
}
return count;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
or
To solve it in place, we use 2 bits to store 2 states:
[2nd bit, 1st bit] = [next state, current state]
- 00 dead (next) <- dead (current)
- 01 dead (next) <- live (current)
- 10 live (next) <- dead (current)
- 11 live (next) <- live (current) In the beginning, every cell is either 00 or 01. Notice that 1st state is independent of 2nd state. Imagine all cells are instantly changing from the 1st to the 2nd state, at the same time. Let's count # of neighbors from 1st state and set 2nd state bit. Since every 2nd state is by default dead, no need to consider transition 01 -> 00. In the end, delete every cell's 1st state by doing >> 1. For each cell's 1st bit, check the 8 pixels around itself, and set the cell's 2nd bit.
Transition 01 -> 11: when board == 1 and lives >= 2 && lives <= 3. Transition 00 -> 10: when board == 0 and lives == 3. To get the current state, simply do
board[i][j] & 1 To get the next state, simply do
board[i][j] >> 1 Hope this helps!
class Solution {
public void gameOfLife(int[][] board) {
if (board == null || board.length == 0) return;
int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int lives = liveNeighbors(board, m, n, i, j);
// In the beginning, every 2nd bit is 0;
// So we only need to care about when will the 2nd bit become 1.
if (board[i][j] == 1 && lives >= 2 && lives <= 3) {
board[i][j] = 3; // Make the 2nd bit 1: 01 ---> 11
}
if (board[i][j] == 0 && lives == 3) {
board[i][j] = 2; // Make the 2nd bit 1: 00 ---> 10
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
board[i][j] >>= 1; // Get the 2nd state.
}
}
}
public int liveNeighbors(int[][] board, int m, int n, int i, int j) {
int lives = 0;
for (int x = Math.max(i - 1, 0); x <= Math.min(i + 1, m - 1); x++) {
for (int y = Math.max(j - 1, 0); y <= Math.min(j + 1, n - 1); y++) {
lives += board[x][y] & 1;
}
}
lives -= board[i][j] & 1;
return lives;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 总结
- 分析出几种情况,然后分别对各个情况实现


