 二叉搜索子树的最大键值和Java
二叉搜索子树的最大键值和Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一棵以 root 为根的 二叉树 ,请你返回 任意 二叉搜索子树的最大键值和。
二叉搜索树的定义如下:
任意节点的左子树中的键值都 小于 此节点的键值。 任意节点的右子树中的键值都 大于 此节点的键值。 任意节点的左子树和右子树都是二叉搜索树。
示例 1:
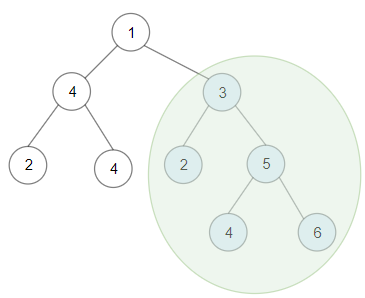
输入:root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出:20
解释:键值为 3 的子树是和最大的二叉搜索树。
示例 2:
输入:root = [4,3,null,1,2]
输出:2
解释:键值为 2 的单节点子树是和最大的二叉搜索树。
示例 3:
输入:root = [-4,-2,-5]
输出:0
解释:所有节点键值都为负数,和最大的二叉搜索树为空。
示例 4:
输入:root = [2,1,3]
输出:6
示例 5:
输入:root = [5,4,8,3,null,6,3]
输出:7
提示:
- 每棵树有 1 到 40000 个节点。
- 每个节点的键值在 [-4 * 10^4 , 4 * 10^4] 之间。
# 思路
int[] res = new int[4];
后序遍历
# 解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
//全局变量,记录 BST 最大节点之和
int maxSum = 0;
public int maxSumBST(TreeNode root) {
traverse(root);
return maxSum;
}
public int[] traverse(TreeNode root) {
if (root == null) {
return new int[]{
1, Integer.MAX_VALUE, Integer.MIN_VALUE, 0
};
}
//递归计算左右子树
int[] left = traverse(root.left);
int[] right = traverse(root.right);
/**
* res[0] 记录以 root 为根的二叉树是否是 BST,若为1则说明是 BST,若为0则说明不是 BST
* res[1] 记录以 root 为根的二叉树所有节点中的最小值
* res[2] 记录以 root 为根的二叉树所有节点中的最大值
* res[3] 记录以 root 为根的二叉树所有节点值之和
*/
/************* 后序遍历位置 ****************/
int[] res = new int[4];
//这个 if 在判断以 root 为根的二叉树是不是 BST
//BST的根节点是大于左子树的最大值,小于右子树的最小值
if (left[0] == 1 && right[0] == 1 &&
root.val > left[2] && root.val < right[1]) {
//以 root 为根的二叉树是 BST
res[0] = 1;
//计算以 root 为根的这棵 BST 的最小值
res[1] = Math.min(left[1], root.val);
//计算以 root 为根的这棵 BST 的最大值
res[2] = Math.max(right[2], root.val);
//计算以 root 为根的这棵 BST 所有节点之和
res[3] = left[3] + right[3] + root.val;
//更新全局变量
maxSum = Math.max(maxSum, res[3]);
} else {
//以 root 为根的二叉树不是 BST
res[0] = 0;
}
/*****************************************/
return res;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
# 总结
- 分析出几种情况,然后分别对各个情况实现


