题目

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

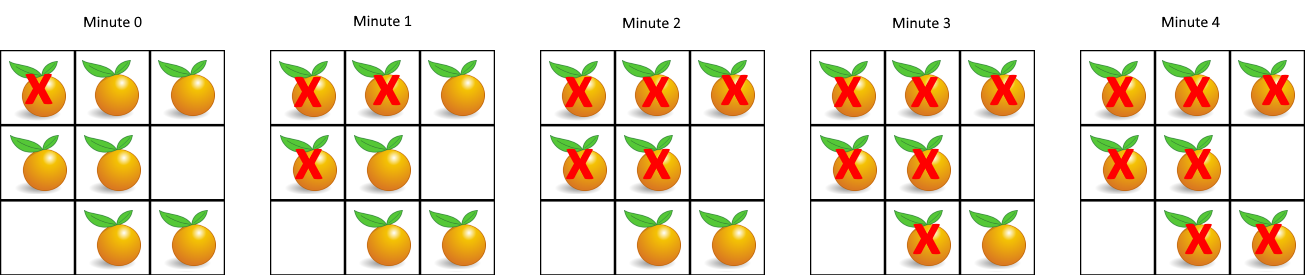
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] 仅为 0、1 或 2

思路

dfs

解法

class Solution {
    
    int[][] grid;
    public int orangesRotting(int[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }

        this.grid = grid;    
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 2) {
                    dfs(i, j, 2); // 开始传染
                } 
            }
        }

        // 经过dfs后，grid数组中记录了每个橘子被传染时的路径长度，找出最大的长度即为腐烂全部橘子所用的时间。
        int maxLevel = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 1) {
                    return -1; // 若有新鲜橘子未被传染到，直接返回-1
                } else {
                    maxLevel = Math.max(maxLevel, grid[i][j]);
                }
            }
        }

        return maxLevel == 0? 0: maxLevel - 2; 
    }

    private void dfs(int i, int j, int level) { // level用来记录传染路径的长度（当然最后要减2）
        if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length ) {
            return;
        }
        if (grid[i][j] != 1 && grid[i][j] < level) { // 只有新鲜橘子或者传播路径比当前路径长的橘子，才继续进行传播。
            return;
        } 
   
        grid[i][j] = level; // 将传染路径的长度存到grid[i][j]中
        level++;
        dfs(i - 1, j, level);
        dfs(i + 1, j, level);
        dfs(i, j - 1, level);
        dfs(i, j + 1, level);
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现