 完美矩形Java
完美矩形Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一个数组 rectangles ,其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ,右上顶点是 (ai, bi) 。
如果所有矩形一起精确覆盖了某个矩形区域,则返回 true ;否则,返回 false 。
示例 1:
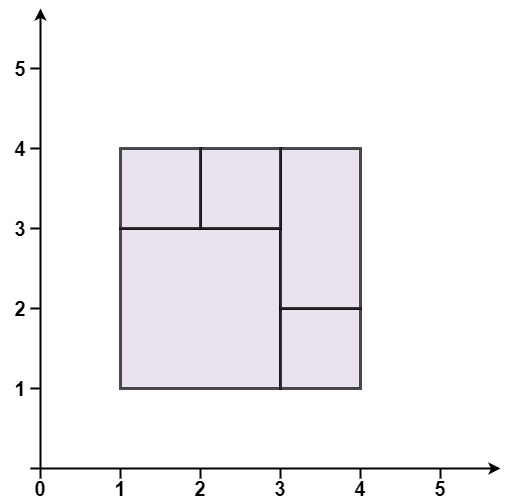
输入:rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出:true
解释:5 个矩形一起可以精确地覆盖一个矩形区域。
示例 2:
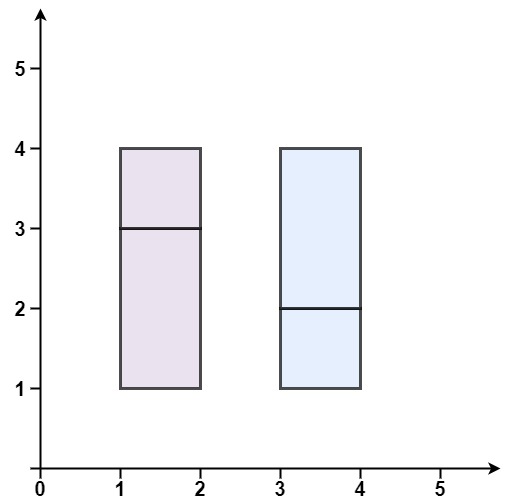
输入:rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出:false
解释:两个矩形之间有间隔,无法覆盖成一个矩形。
示例 3:
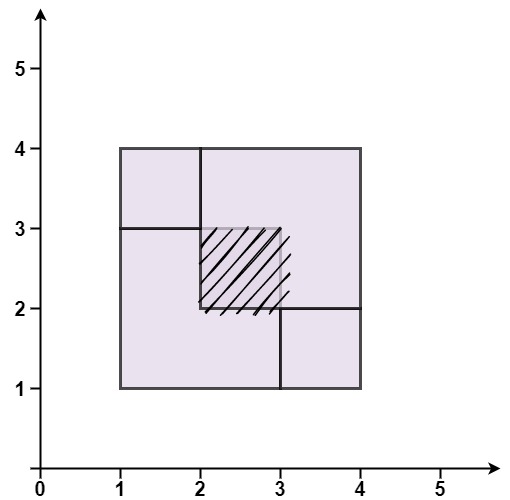
输入:rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] 输出:false
解释:因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
提示:
- 1 <= rectangles.length <= 2 * 104
- rectangles[i].length == 4
- -105 <= xi, yi, ai, bi <= 105
# 思路
如果是完美矩形 那么一定满足两点: (1)最左下 最左上 最右下 最右上 的四个点只出现一次 其他点成对出现 (2)四个点围城的矩形面积 = 小矩形的面积之和
# 解法
class Solution {
// 如果是完美矩形 那么一定满足两点: (1)最左下 最左上 最右下 最右上 的四个点只出现一次 其他点成对出现 (2)四个点围城的矩形面积 = 小矩形的面积之和
public boolean isRectangleCover(int[][] rectangles) {
int left = Integer.MAX_VALUE;
int right = Integer.MIN_VALUE;
int top = Integer.MIN_VALUE;
int bottom = Integer.MAX_VALUE;
int n = rectangles.length;
Set<String> set = new HashSet<>();
int sumArea = 0;
for (int i = 0; i < n; i++) {
//获取四个点的坐标
left = Math.min(left, rectangles[i][0]);
bottom = Math.min(bottom, rectangles[i][1]);
right = Math.max(right, rectangles[i][2]);
top = Math.max(top, rectangles[i][3]);
//计算总小矩形的面积
sumArea += (rectangles[i][3] - rectangles[i][1]) * (rectangles[i][2] - rectangles[i][0]);
//分别记录小矩形的坐标
String lt = rectangles[i][0] + " " + rectangles[i][3];
String lb = rectangles[i][0] + " " + rectangles[i][1];
String rt = rectangles[i][2] + " " + rectangles[i][3];
String rb = rectangles[i][2] + " " + rectangles[i][1];
//如果有就移除 没有就加入
if (!set.contains(lt)) set.add(lt);
else set.remove(lt);
if (!set.contains(lb)) set.add(lb);
else set.remove(lb);
if (!set.contains(rt)) set.add(rt);
else set.remove(rt);
if (!set.contains(rb)) set.add(rb);
else set.remove(rb);
}
//最后只剩4个大矩形坐标且面积相等即为完美矩形
if (set.size() == 4 && set.contains(left + " " + top) && set.contains(left + " " + bottom) && set.contains(right + " " + bottom) && set.contains(right + " " + top)) {
return sumArea == (right - left) * (top - bottom);
}
return false;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 总结
- 分析出几种情况,然后分别对各个情况实现


