 对角线遍历 IIJava
对角线遍历 IIJava
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一个列表 nums ,里面每一个元素都是一个整数列表。请你依照下面各图的规则,按顺序返回 nums 中对角线上的整数。
示例 1:
输入:nums = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,4,2,7,5,3,8,6,9]
示例 2:
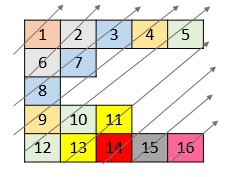
输入:nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
输出:[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]
示例 3:
输入:nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
输出:[1,4,2,5,3,8,6,9,7,10,11]
示例 4:
输入:nums = [[1,2,3,4,5,6]]
输出:[1,2,3,4,5,6]
提示:
- 1 <= nums.length <= 10^5
- 1 <= nums[i].length <= 10^5
- 1 <= nums[i][j] <= 10^9
- nums 中最多有 10^5 个数字。
# 思路
这题目最少也要把列表所有元素都遍历一遍,那怎么只遍历一遍呢? 看这个遍历顺序,然后就想到了用栈,在按行列遍历的过程把元素依次入栈,pop出来的时候就是题目要求的遍历顺序了
# 解法
public class Solution {
public int[] findDiagonalOrder(List<List<Integer>> nums) {
int n = nums.size();
//计算最大对角线之和
int max = 0;
for(int r = 0; r < n; r ++)
max = Math.max(max, r + nums.get(r).size());
//stack[sum] 表示 行号r + 列号j == sum 的所有元素,并且行号越小的元素,越先入栈
Stack<Integer>[] stacks = new Stack[max];
for(int i = 0; i < max; i ++)
stacks[i] = new Stack<>();
//开始逐行逐列,将所有元素放入对应的栈中
int size = 0;
for(int i = 0; i < n; i ++)
for(int j = 0; j < nums.get(i).size(); j ++) {
stacks[i + j].push(nums.get(i).get(j));
size ++;
}
// 因为前面入栈的过程保证了相同对角线上的所有元素,行数越大的越后入栈;
// 所以pop的时候越早被pop出来,也就是按照了题目要求的顺序pop了出来
int[] res = new int[size];
int index = 0;
for(int i = 0; i < max; i ++)
while(!stacks[i].isEmpty()) res[index++] = stacks[i].pop();
return res;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 总结
- 分析出几种情况,然后分别对各个情况实现


