 互质树Java
互质树Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一个 n 个节点的树(也就是一个无环连通无向图),节点编号从 0 到 n - 1 ,且恰好有 n - 1 条边,每个节点有一个值。树的 根节点 为 0 号点。
给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值,edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。
当 gcd(x, y) == 1 ,我们称两个数 x 和 y 是 互质的 ,其中 gcd(x, y) 是 x 和 y 的 最大公约数 。
从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。
请你返回一个大小为 n 的数组 ans ,其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ,如果不存在这样的祖先节点,ans[i] 为 -1 。
示例 1:
输入:nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出:[-1,0,0,1]
解释:上图中,每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的(gcd(2,3) == 1)。
- 节点 2 有两个祖先节点,分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的(gcd(3,3) == 3)但节点 0 的值是互质的(gcd(2,3) == 1),所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点,分别是节点 1 和节点 0 。它与节点 1 互质(gcd(3,2) == 1),所以节点 1 是离它最近的符合要求的祖先节点。
示例 2:
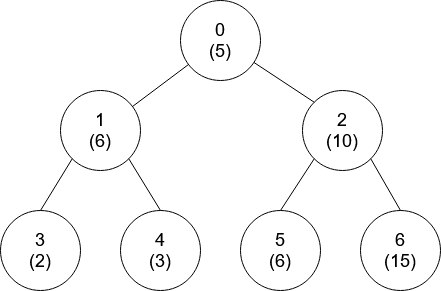
输入:nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出:[-1,0,-1,0,0,0,-1]
提示:
- nums.length == n
- 1 <= nums[i] <= 50
- 1 <= n <= 105
- edges.length == n - 1
- edges[j].length == 2
- 0 <= uj, vj < n
- uj != vj
# 思路
dfs
# 解法
class Solution {
int[] nums;
List<Integer>[] g;
int[] ans;
public int[] getCoprimes(int[] nums, int[][] edges) {
this.nums = nums;
ans = new int[nums.length];
ans[0] = -1;
g = new List[nums.length];
Arrays.setAll(g, e -> new ArrayList<>());
for (int[] edge : edges) {
g[edge[0]].add(edge[1]);
g[edge[1]].add(edge[0]);
}
// 初始化list和map
LinkedList<Integer> grandList = new LinkedList<>();
grandList.add(nums[0]);
HashMap<Integer, Deque<Integer>> map = new HashMap<>();
Deque<Integer> deque = new ArrayDeque<>();
deque.add(0);
map.put(nums[0], deque);
dfs(0, -1, grandList, map);
return ans;
}
private void dfs(int son, int fa, LinkedList<Integer> grandLink, HashMap<Integer, Deque<Integer>> map) {
List<Integer> nodes = g[son];
for (int node : nodes) {
if (node == fa) continue;
int nodeVal = nums[node];
boolean flag = false;
for (int v : grandLink) {
if (gcd(v, nodeVal) == 1) {
ans[node] = map.get(v).getFirst();
flag = true;
break;
}
}
if (!flag) ans[node] = -1;
Deque<Integer> deque = map.get(nodeVal);
int removedIndex = -1;
if (deque == null) {
deque = new ArrayDeque<>();
deque.add(node);
map.put(nodeVal, deque);
grandLink.addFirst(nodeVal);
} else {
deque.addFirst(node);
removedIndex = grandLink.indexOf(nodeVal);
if (removedIndex != 0) {
grandLink.remove(removedIndex);
grandLink.addFirst(nodeVal);
}
}
dfs(node, son, grandLink, map);
// 恢复原状态
if (removedIndex == -1) grandLink.pollFirst();
else if (removedIndex != 0) {
grandLink.pollFirst();
grandLink.add(removedIndex, nodeVal);
}
Deque<Integer> integerDeque = map.get(nodeVal);
if (integerDeque.size() == 1) map.remove(nodeVal);
else integerDeque.removeFirst();
}
}
private int gcd(int a, int b) {
return (a % b == 0) ? b : gcd(b,a % b );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
# 总结
- 分析出几种情况,然后分别对各个情况实现


