题目

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

• ri 行上的所有单元格，加 1 。
• ci 列上的所有单元格，加 1 。 给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

示例 1：

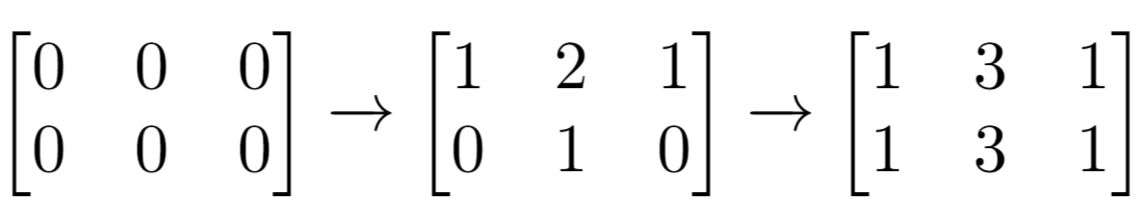
输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2：

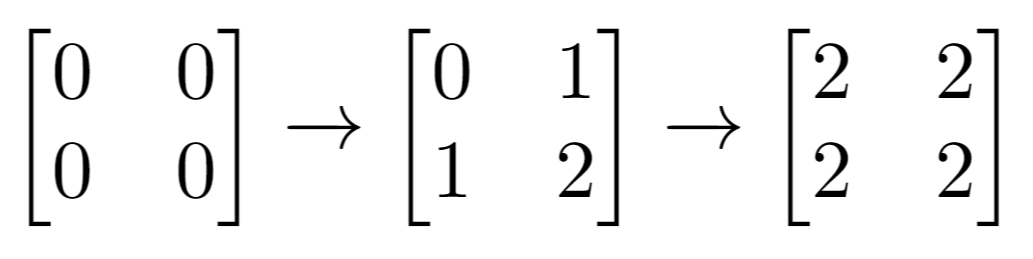
输入：m = 2, n = 2, indices = [[1,1],[0,0]]
输出：0
解释：最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

提示：

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

进阶：你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗？

思路

boolean[] r = new boolean[n]; boolean[] c = new boolean[m];

解法

class Solution {
    public int oddCells(int n, int m, int[][] indices) {
        boolean[] r = new boolean[n];
        boolean[] c = new boolean[m];
        int i;
        for (i = 0; i < indices.length; i++) {
            r[indices[i][0]] = !r[indices[i][0]];
            c[indices[i][1]] = !c[indices[i][1]];
        }
        int rr = 0, cc = 0;
        for (i = 0; i < r.length; i++) {
            if(r[i])rr++;
        }
        for (i = 0; i < c.length; i++) {
            if(c[i])cc++;
        }
        return rr * m + cc * n - rr * cc * 2;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现