 移除子树后的二叉树高度Java
移除子树后的二叉树高度Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一棵 二叉树 的根节点 root ,树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。
你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
- 从树中 移除 以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不 等于根节点的值。 返回一个长度为 m 的数组 answer ,其中 answer[i] 是执行第 i 个查询后树的高度。
注意:
- 查询之间是独立的,所以在每个查询执行后,树会回到其 初始 状态。
- 树的高度是从根到树中某个节点的 最长简单路径中的边数 。
示例 1:
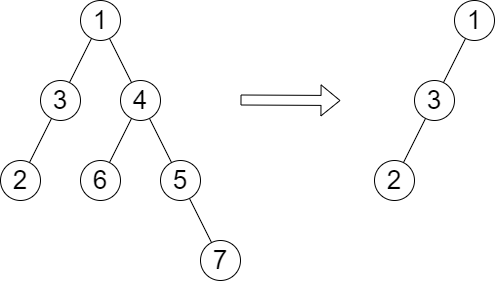
输入:root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出:[2]
解释:上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2(路径为 1 -> 3 -> 2)。
示例 2:
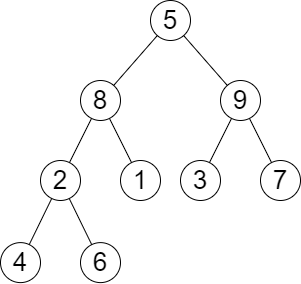
输入:root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出:[3,2,3,2]
解释:执行下述查询:
- 移除以 3 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 4)。
- 移除以 2 为根节点的子树。树的高度变为 2(路径为 5 -> 8 -> 1)。
- 移除以 4 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 6)。
- 移除以 8 为根节点的子树。树的高度变为 2(路径为 5 -> 9 -> 3)。
提示:
- 树中节点的数目是 n
- 2 <= n <= 105
- 1 <= Node.val <= n
- 树中的所有值 互不相同
- m == queries.length
- 1 <= m <= min(n, 104)
- 1 <= queries[i] <= n
- queries[i] != root.val
# 思路
用集合存下树的层次结构,在要删除的节点的那层找到高度最大的节点,如果就是要删除的选第二高的结点的高度加上这一层的层数减一,如果不是要删除的就选最高的加上这一层的层数减一
# 解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int[] treeQueries(TreeNode root, int[] queries) {
List<List<Integer>> levels = new ArrayList<>();
Map<Integer,Integer> height = new HashMap<>();
Map<Integer, Integer> level = new HashMap<>();
dfs(root, 0, height, level, levels);
for(List<Integer> list : levels) Collections.sort(list, (o1, o2) -> o2-o1);
int n = queries.length;
int[] ans = new int[n];
for(int i = 0; i < n; i++){
int l = level.get(queries[i]);
int h = height.get(queries[i]);
List<Integer> list = levels.get(l);
if(list.get(0) != h) ans[i] = list.get(0) + l - 1;
else{
if(list.size() == 1) ans[i] = l - 1;
else ans[i] = list.get(1) + l - 1;
}
}
return ans;
}
public int dfs(TreeNode root, int l, Map<Integer,Integer> height, Map<Integer, Integer> level, List<List<Integer>> levels){
if(root == null) return 0;
level.put(root.val, l);
if(levels.size() <= l) levels.add(new ArrayList<>());
int max = Math.max(dfs(root.left, l + 1, height, level, levels), dfs(root.right, l + 1, height, level, levels)) + 1;
height.put(root.val, max);
levels.get(l).add(max);
return max;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 总结
- 分析出几种情况,然后分别对各个情况实现


