题目

有一棵 n 个节点的无向树，节点编号为 0 到 n - 1 。

给你一个长度为 n 下标从 0 开始的整数数组 nums ，其中 nums[i] 表示第 i 个节点的值。同时给你一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 与 bi 之间有一条边。

你可以 删除 一些边，将这棵树分成几个连通块。一个连通块的 价值 定义为这个连通块中 所有 节点 i 对应的 nums[i] 之和。

你需要删除一些边，删除后得到的各个连通块的价值都相等。请返回你可以删除的边数 最多 为多少。

示例 1：

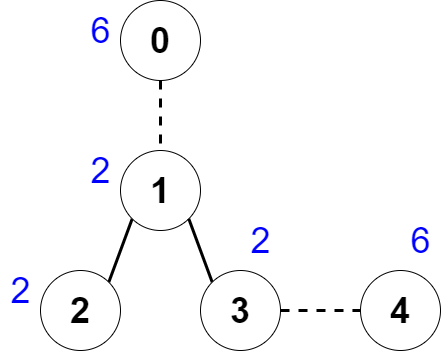
输入：nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：2
解释：上图展示了我们可以删除边 [0,1] 和 [3,4] 。得到的连通块为 [0] ，[1,2,3] 和 [4] 。每个连通块的价值都为 6 。可以证明没有别的更好的删除方案存在了，所以答案为 2 。
示例 2：

输入：nums = [2], edges = []
输出：0
解释：没有任何边可以删除。

提示：

• 1 <= n <= 2 * 10⁴
• nums.length == n
• 1 <= nums[i] <= 50
• edges.length == n - 1
• edges[i].length == 2
• 0 <= edges[i][0], edges[i][1] <= n - 1
• edges 表示一棵合法的树。

思路

• 1.每个块都相等->每个块的和是总和的因子->枚举因子
• 2.层序遍历树，每个节点保存其父节点
• 3.倒着遍历层序，如果该节点值大于当前枚举的因子->该因子不能成立，等于->连通块+1，小于->将该连通块的值加到当前节点的父节点上去（一个节点只有当儿子遍历完后才能继续向上贡献，因此采用层序）
• 4.提前对因子排序，当因子小的时候，得到的结果一定是比大因子大的，因此如果此次枚举出结果，可以直接返回

解法

class Solution {
    public int componentValue(int[] nums, int[][] edges) {
        int n = nums.length;
        if (n == 1) {
            return 0;
        }
        boolean[] v = new boolean[n];
        Map<Integer, List<Integer>> map = new HashMap<>();
        int sum = 0;
        int min = 99;
        for (int x : nums) {
            sum += x;
            min = Math.min(min, x);
        }
        List<Integer> list = new ArrayList<>();
        for (int i = min; i <= (int) Math.sqrt(sum); i++) {
            if (sum % i == 0) {
                list.add(i);
                list.add(sum / i);
            }
        }
        Collections.sort(list);
        for (int[] e : edges) {
            map.putIfAbsent(e[0], new ArrayList<>());
            map.putIfAbsent(e[1], new ArrayList<>());
            map.get(e[0]).add(e[1]);
            map.get(e[1]).add(e[0]);
        }
        List<List<int[]>> level = new ArrayList<>();
        List<int[]> zero = new ArrayList<>();
        zero.add(new int[]{0, 0});
        Queue<Integer> que = new LinkedList<>();
        que.offer(0);
        while (!que.isEmpty()) {
            List<int[]> tmp = new ArrayList<>();
            for (int i = que.size(); i > 0; i--) {
                int p = que.poll();
                v[p] = true;
                for (int x : map.get(p)) {
                    if (v[x]) {
                        continue;
                    }
                    tmp.add(new int[]{x, p});
                    que.offer(x);
                }
            }
            if (tmp.size() != 0) {
                level.add(tmp);
            }
        }
        int ans = 0;
        for (Integer x : list) {
            int[] w = new int[n];
            for (int i = 0; i < n; i++) {
                w[i] = nums[i];
            }
            boolean flag = false;
            int t = 0;
            for (int i = level.size() - 1; i >= 0; i--) {
                for (int[] j : level.get(i)) {
                    if (w[j[0]] > x) {
                        flag = true;
                        break;
                    } else if (w[j[0]] == x) {
                        t++;
                    } else {
                        w[j[1]] += w[j[0]];
                    }
                }
                if (flag) {
                    break;
                }
            }
            if (flag) {
                continue;
            }
            ans = Math.max(ans, t);
            if (ans > 0) {
                return ans;
            }
        }
        return ans;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现