题目

有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。

返回在路径距离限制为 distanceThreshold 以内可到达城市最少的城市。如果有多个这样的城市，则返回编号最大的城市。

注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

示例 1：

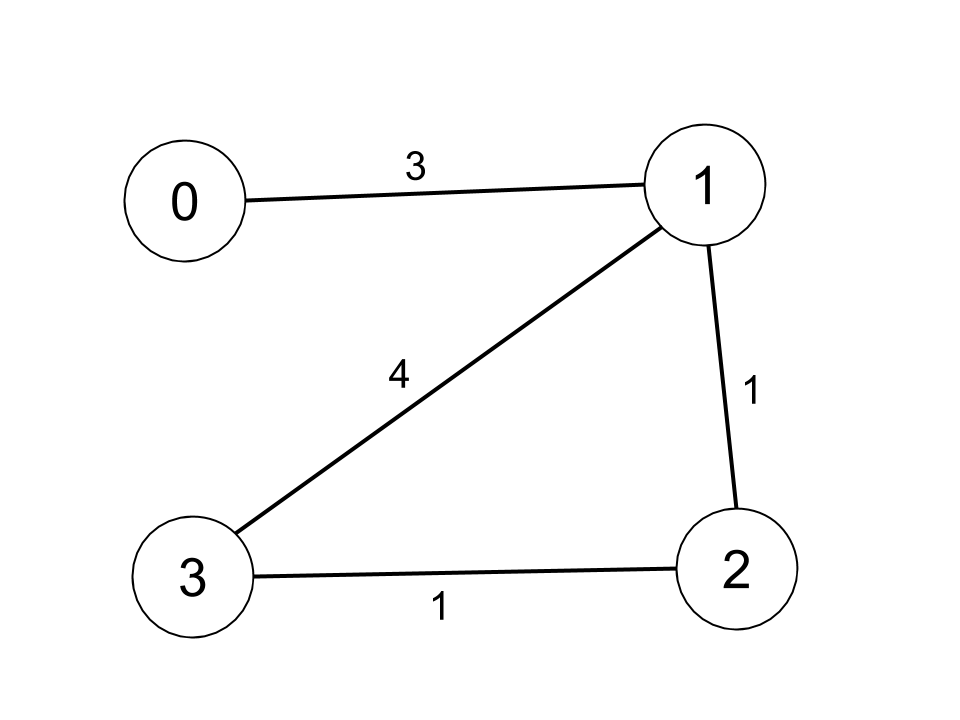
输入：n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出：3
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是：
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市，但是我们必须返回城市 3，因为它的编号最大。

示例 2：

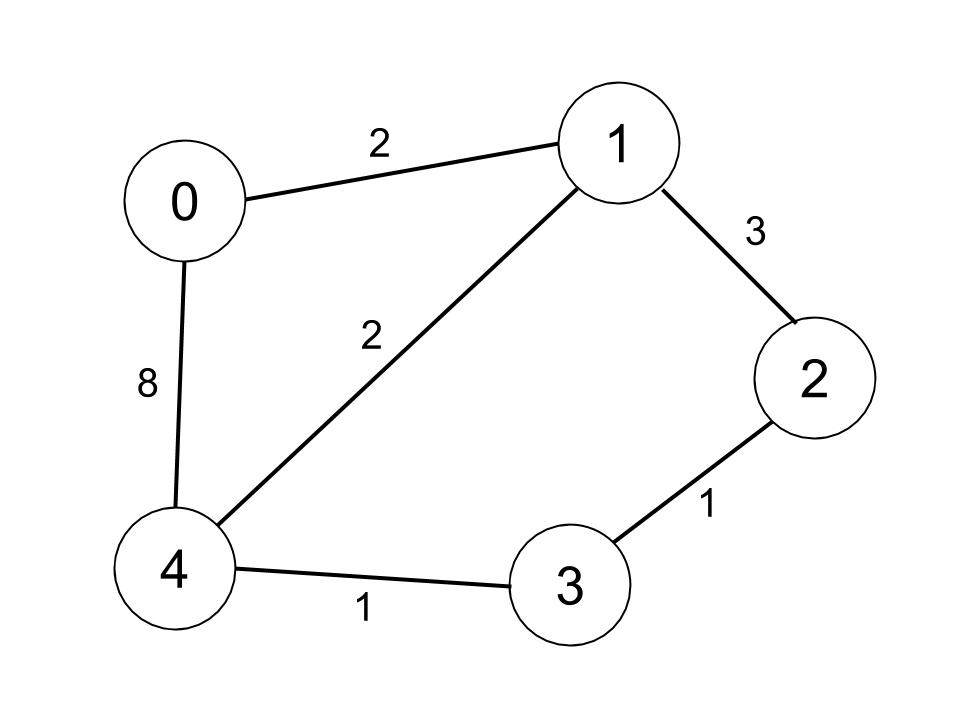
输入：n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出：0
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是：
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。

提示：

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• 所有 (fromi, toi) 都是不同的。

思路

初始化任意两点之间距离

解法

class Solution {
    public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        // 初始化任意两点之间距离
        int[][] distance = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(distance[i], Integer.MAX_VALUE);
            distance[i][i] = 0;
        }
        for (int[] edge : edges) {
            distance[edge[0]][edge[1]] = edge[2];
            distance[edge[1]][edge[0]] = edge[2];
        }
        // Floyd求任意ij之间最短路径
        for (int k = 0; k < n; k++)
            for (int i = 0; i < n ; i++)
                for (int j = 0; j < n; j++)
                    if (distance[i][k] != Integer.MAX_VALUE &&
                        distance[k][j] != Integer.MAX_VALUE)
                        distance[i][j] = Math.min(distance[i][j], distance[i][k] + distance[k][j]);

        int min = Integer.MAX_VALUE; // 记录最小可到达数量
        int res = -1; // 记录对应城市
        for (int i = 0; i < n; i++) {
            int count = 0; // 记录城市i符合要求的可到达城市数量
            for (int j = 0; j < n ; j++)
                if (distance[i][j] <= distanceThreshold)
                    count++;
            if (count <= min) {
                min = count;
                res = i;
            }
        }
        return res;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现