题目

两位玩家分别扮演猫和老鼠，在一张 无向 图上进行游戏，两人轮流行动。

图的形式是：graph[a] 是一个列表，由满足 ab 是图中的一条边的所有节点 b 组成。

老鼠从节点 1 开始，第一个出发；猫从节点 2 开始，第二个出发。在节点 0 处有一个洞。

在每个玩家的行动中，他们 必须 沿着图中与所在当前位置连通的一条边移动。例如，如果老鼠在节点 1 ，那么它必须移动到 graph[1] 中的任一节点。

此外，猫无法移动到洞中（节点 0）。

然后，游戏在出现以下三种情形之一时结束：

• 如果猫和老鼠出现在同一个节点，猫获胜。

• 如果老鼠到达洞中，老鼠获胜。

• 如果某一位置重复出现（即，玩家的位置和移动顺序都与上一次行动相同），游戏平局。 给你一张图 graph ，并假设两位玩家都都以最佳状态参与游戏：

• 如果老鼠获胜，则返回 1；

• 如果猫获胜，则返回 2；

• 如果平局，则返回 0 。

示例 1：

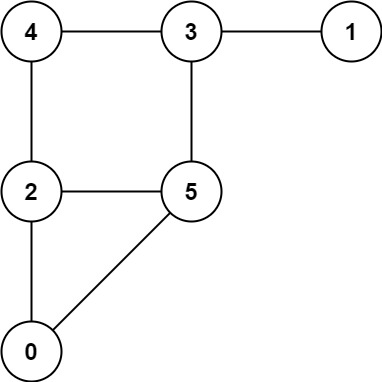
输入：graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
输出：0

示例 2：

输入：graph = [[1,3],[0],[3],[0,2]]
输出：1

提示：

• 3 <= graph.length <= 50
• 1 <= graph[i].length < graph.length
• 0 <= graph[i][j] < graph.length
• graph[i][j] != i
• graph[i] 互不相同
• 猫和老鼠在游戏中总是可以移动

思路

Queue<int[]> queue = new ArrayDeque<int[]>();

解法

class Solution {
    public static final int HOLE = 0, MOUSE_START = 1, CAT_START = 2;
    public static final int MOUSE_TURN = 0, CAT_TURN = 1;
    public static final int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
    private int n;
    private int[][] graph;
    private int[][][] degrees;
    private int[][][] results;

    public int catMouseGame(int[][] graph) {
        this.n = graph.length;
        this.graph = graph;
        this.degrees = new int[n][n][2];
        this.results = new int[n][n][2];
        for (int i = 0; i < n; i++) {
            for (int j = 1; j < n; j++) {
                degrees[i][j][MOUSE_TURN] = graph[i].length;
                degrees[i][j][CAT_TURN] = graph[j].length;
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j : graph[HOLE]) {
                degrees[i][j][CAT_TURN]--;
            }
        }
        Queue<int[]> queue = new ArrayDeque<int[]>();
        for (int i = 1; i < n; i++) {
            results[i][i][MOUSE_TURN] = CAT_WIN;
            results[i][i][CAT_TURN] = CAT_WIN;
            queue.offer(new int[]{i, i, MOUSE_TURN});
            queue.offer(new int[]{i, i, CAT_TURN});
        }
        for (int j = 1; j < n; j++) {
            results[HOLE][j][MOUSE_TURN] = MOUSE_WIN;
            results[HOLE][j][CAT_TURN] = MOUSE_WIN;
            queue.offer(new int[]{HOLE, j, MOUSE_TURN});
            queue.offer(new int[]{HOLE, j, CAT_TURN});
        }
        while (!queue.isEmpty()) {
            int[] state = queue.poll();
            int mouse = state[0], cat = state[1], turn = state[2];
            int result = results[mouse][cat][turn];
            List<int[]> prevStates = getPrevStates(mouse, cat, turn);
            for (int[] prevState : prevStates) {
                int prevMouse = prevState[0], prevCat = prevState[1], prevTurn = prevState[2];
                if (results[prevMouse][prevCat][prevTurn] == UNKNOWN) {
                    boolean winState = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
                    if (winState) {
                        results[prevMouse][prevCat][prevTurn] = result;
                        queue.offer(new int[]{prevMouse, prevCat, prevTurn});
                    } else {
                        degrees[prevMouse][prevCat][prevTurn]--;
                        if (degrees[prevMouse][prevCat][prevTurn] == 0) {
                            results[prevMouse][prevCat][prevTurn] = result;
                            queue.offer(new int[]{prevMouse, prevCat, prevTurn});
                        }
                    }
                }
            }
        }
        return results[MOUSE_START][CAT_START][MOUSE_TURN];
    }

    private List<int[]> getPrevStates(int mouse, int cat, int turn) {
        List<int[]> prevStates = new ArrayList<int[]>();
        int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
        if (prevTurn == CAT_TURN) {
            for (int prevCat : graph[cat]) {
                if (prevCat != HOLE) {
                    prevStates.add(new int[]{mouse, prevCat, prevTurn});
                }
            }
        } else {
            for (int prevMouse : graph[mouse]) {
                prevStates.add(new int[]{prevMouse, cat, prevTurn});
            }
        }
        return prevStates;
    }
}

总结

• 分析出几种情况，然后分别对各个情况实现