 矩形面积 IIJava
矩形面积 IIJava
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
给你一个轴对齐的二维数组 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标, (xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。
返回 总面积 。因为答案可能太大,返回 109 + 7 的 模 。
示例 1:
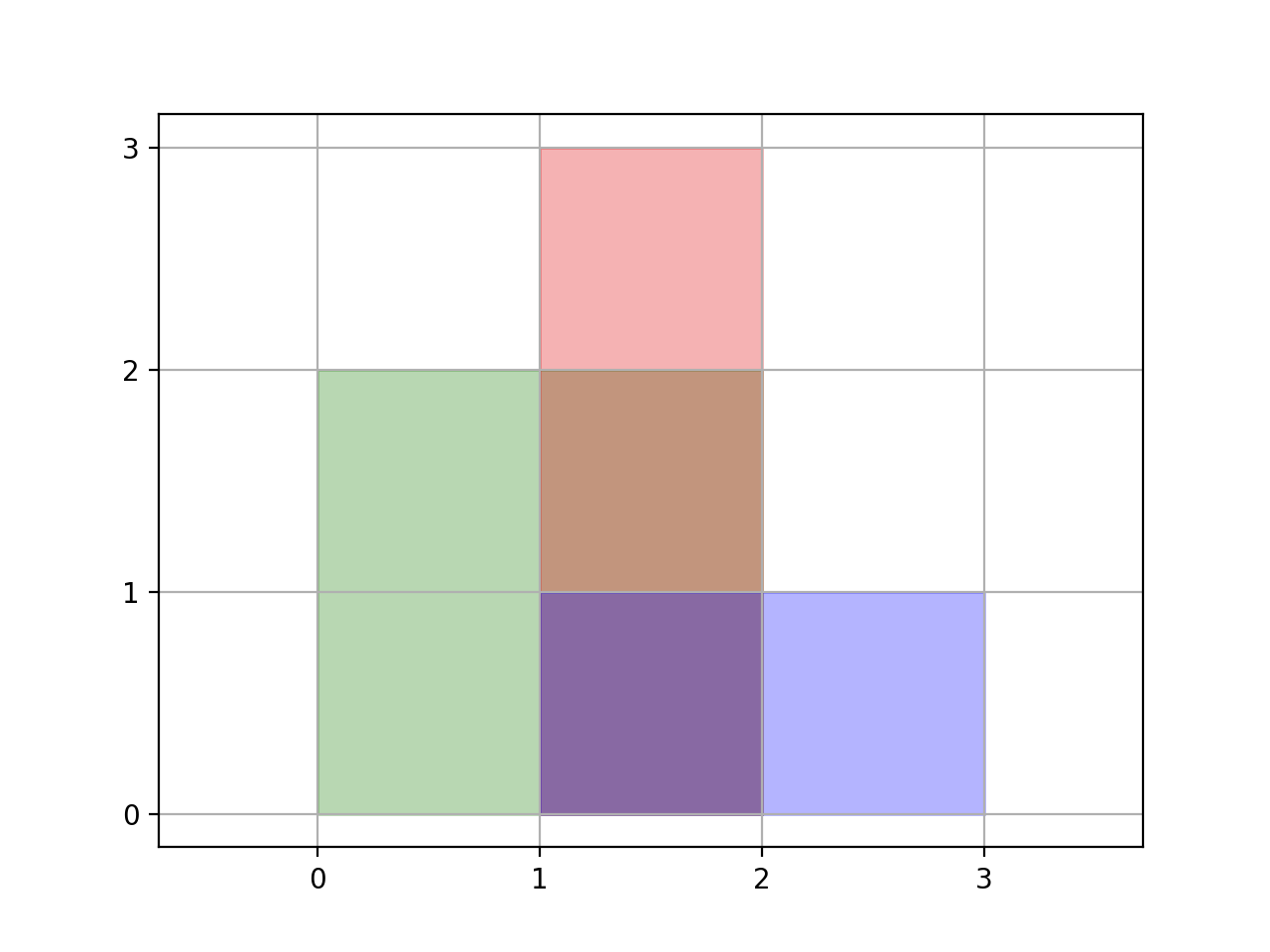
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为 6 的区域。
从(1,1)到(2,2),绿色矩形和红色矩形重叠。
从(1,0)到(2,3),三个矩形都重叠。
示例 2:
- 输入:rectangles = [[0,0,1000000000,1000000000]]
- 输出:49
- 解释:答案是 1018 对 (109 + 7) 取模的结果, 即 49 。
提示:
- 1 <= rectangles.length <= 200
- rectanges[i].length = 4
- 0 <= xi1, yi1, xi2, yi2 <= 109
# 思路
线段树
# 解法
class Solution {
int mod=(int)1e9+7;
public int rectangleArea(int[][] rectangles) {
int map1[]=compress(rectangles,0,2),map2[]=compress(rectangles,1,3);
long ans=0;
for(int i=0;i<map1.length-1;i++){
int count[]=new int[map2.length+5];
for(int j=0;j<rectangles.length;j++){
if(i>=rectangles[j][0]&&i<rectangles[j][2]){
count[rectangles[j][1]]++;
count[rectangles[j][3]]--;
}
}
long d=map1[i+1]-map1[i];
if(count[0]>0){ans+=d*(map2[1]-map2[0]);}
for(int j=1;j<map2.length;j++){
count[j]+=count[j-1];
if(count[j]>0){ans+=d*(map2[j+1]-map2[j]);}
}
}
return (int)(ans%mod);
}
int[] compress(int r[][],int idx1,int idx2){
TreeSet<Integer> set=new TreeSet<>();
for(int i=0;i<r.length;i++){
set.add(r[i][idx1]);
set.add(r[i][idx2]);
}
Map<Integer,Integer> map=new HashMap<>();
int ans[]=new int[set.size()];
int p=0;
for(int a:set){
ans[p]=a;
map.put(a,p);
p++;
}
for(int i=0;i<r.length;i++){
r[i][idx1]=map.get(r[i][idx1]);
r[i][idx2]=map.get(r[i][idx2]);
}
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 总结
- 分析出几种情况,然后分别对各个情况实现


