按公因数计算最大组件大小Java

文章发布较早，内容可能过时，阅读注意甄别。

# 题目

给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。返回图中最大连通组件的大小。

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

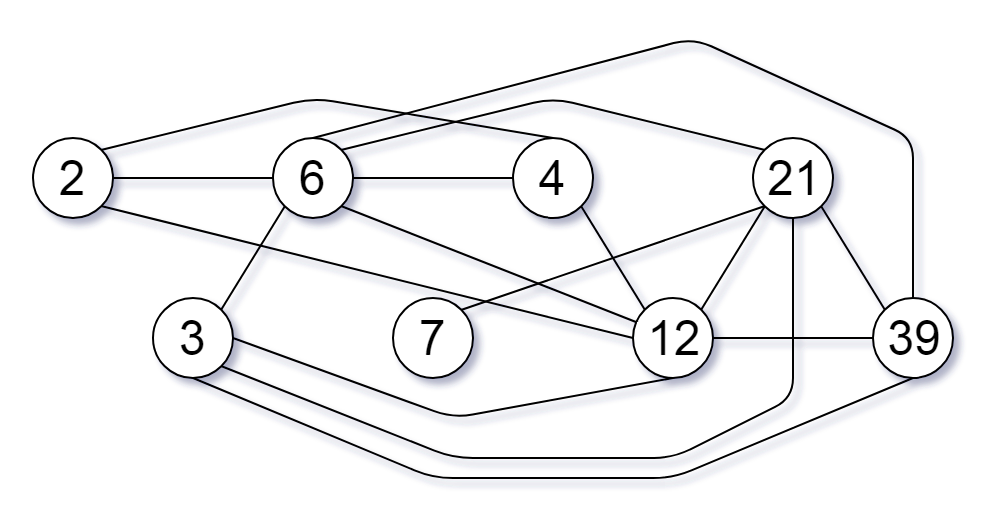
输入：nums = [2,3,6,7,4,12,21,39]
输出：8

提示：

1 <= nums.length <= 2 * 10⁴
1 <= nums[i] <= 10⁵
nums 中所有值都不同

# 思路

Java 并查集

# 解法


class Solution {
    // Java 并查集


    public int largestComponentSize(int[] A) {
        // 获得数组中最大值 
        int max = 0;
        for(int i=0;i<A.length;i++){
            max = Math.max(max, A[i]);
        }
        // System.out.println(max);
        DSU dsu = new DSU(max + 1);
        for(int a: A){
            for(int k=2;k<=Math.sqrt(a);k++){
                if(a%k==0){
                    // 将 a的因子union在一起
                    dsu.union(a,k);
                    dsu.union(a,a/k);
                }
            }
        }
        Map<Integer, Integer> map = new HashMap<>();
        int ans = 1;
        for(int a: A){
            int temp = map.getOrDefault(dsu.find(a),0)+1;
            ans = Math.max(ans, temp);
            map.put(dsu.find(a),temp);
        }
        return ans;
    }
}
class DSU{
    public int[] parent;
    public DSU(int n){
        parent = new int[n];
        for(int i =0;i< n;i++){
            parent[i] = i;
        }
    }
    public int find(int x){
        if(parent[x] !=x) parent[x] = find(parent[x]);
        return parent[x];
    }
    public void union(int x, int y){
        parent[find(x)] = parent[find(y)];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 总结

分析出几种情况，然后分别对各个情况实现

#Java

← 翻转等价二叉树二倍数对数组→