 访问所有节点的最短路径Java
访问所有节点的最短路径Java
文章发布较早,内容可能过时,阅读注意甄别。
# 题目
存在一个由 n 个节点组成的无向连通图,图中的节点按从 0 到 n - 1 编号。
给你一个数组 graph 表示这个图。其中,graph[i] 是一个列表,由所有与节点 i 直接相连的节点组成。
返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止,也可以多次重访节点,并且可以重用边。
示例 1:
输入:graph = [[1,2,3],[0],[0],[0]]
输出:4
解释:一种可能的路径为 [1,0,2,0,3]
示例 2:
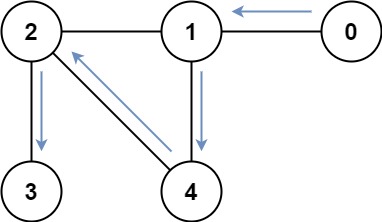
输入:graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出:4
解释:一种可能的路径为 [0,1,4,2,3]
提示:
- n == graph.length
- 1 <= n <= 12
- 0 <= graph[i].length < n
- graph[i] 不包含 i
- 如果 graph[a] 包含 b ,那么 graph[b] 也包含 a
- 输入的图总是连通图
# 思路
Queue<int[]> queue = new LinkedList<int[]>();
# 解法
class Solution {
public int shortestPathLength(int[][] graph) {
int n = graph.length;
int ans = 0;
Queue<int[]> queue = new LinkedList<int[]>();
/*
因为题目规定节点可以重复经过,以前常使用的visited[i]就不能在这里使用,visited[i]: 表示i节点是否被遍历过。
seen[i][j]: 表示i节点在其他节点已经被访问的情况下是否已经被访问过了。
举个例子:seen[1][1100]=true(列号用二进制表示):表示编号为3和2的节点已经被遍历的情况下,节点
1是否已经被遍历了。
*/
boolean[][] seen = new boolean[n][1<<n];
for(int i=0; i<n; i++){
queue.offer(new int[]{i, 1<<i, 0});
seen[i][1<<i] = true;
}
while(!queue.isEmpty()){
int[] cur = queue.poll();
int val = cur[0];
int mask = cur[1];
int dst = cur[2];
if(mask==(1<<n)-1){ //全部节点已经遍历过,返回答案
ans = dst;
break;
}
//搜索相邻的节点
for(int next: graph[val]){
//将mask的第next位置为1
int maskNext = mask|(1<<next);
//避免在图中绕圈
if(!seen[next][maskNext]){
queue.offer(new int[]{next, maskNext, dst+1});
seen[next][maskNext] = true;
}
}
}
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 总结
- 分析出几种情况,然后分别对各个情况实现


